Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fator de Forma

Ver Teoria
Exercício 31245678

Enunciado

Uma pista de patinação no gelo circular com 25   m de diâmetro encontra-se coberta por uma cúpula hemisférica com 35   m de diâmetro.

Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpo negro e estiverem a 0 ° C e 15 ° C , respectivamente, qual é a taxa líquida de transferência de radiação da cúpula para a pista?

Passo 1

O que queremos calcular é a taxa de transferência q 2 → 1 , dada por:

q 2 → 1 = A 2 . F 2 → 1 . σ . T 2 4 - T 1 4

Dessa equação, nós temos tudo, exceto o fator de forma. Então vamos atrás dele!

Passo 2

A ideia aqui é a seguinte:

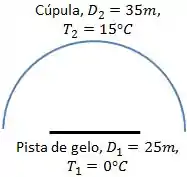
Por se tratar de uma pista plana, nenhuma radiação emitida pela pista é recebida por ela mesma, logo:

F 1 → 1 = 0

Assim, utilizando a regra da adição, temos que:

F 1 → 1 + F 1 → 2 = 1

F 1 → 2 = 1

Utilizando a regra da reciprocidade, o fator de forma F 2 → 1 será dado por:

A 2 . F 2 → 1 = F 1 → 2 . A 1

Como na equação da transferência de calor nós temos o produto A 2 . F 2 → 1 , vou deixar esse produto desse jeito mesmo.

Mas se você preferir calcular F 2 → 1 separadamente, basta passa o termo A 2 para o outro lado, dividindo. Assim:

A 2 . F 2 → 1 = 1 × π D 1 2 4 = π × 25 2 4

A 2 . F 2 → 1 = 491   m 2

Passo 3

Voltando à equação da taxa de transferência de radiação, teremos:

q 2 → 1 = 491 × 5,67 × 10 - 8 × 15 + 273 4 - 0 + 273 4

q 2 → 1 = 3,69 × 10 4   W

Resposta

q 2 → 1 =

Exercícios de Livros Relacionados

A configuração mostrada é usada para calibrar um medidor de fluxo térmico. O medidor tem uma superfície negra com 10 mm de diâmetro, que é mantida a 17°C por uma placa de suporte resfriada com água. O
Uma amostra aquecida eletricamente é mantida com uma temperatura superficial Ta = 500 K. O revestimento da amostra é difuso, porém espectralmente seletivo, com a distribuição da emissividade espectral
Uma pista de patinação no gelo circular com 25m de diâmetro encontra-se coberta por uma cúpula hemisférica com 35m de diâmetro. Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpos
Como mostrado na figura, considere o disco A 1 localizado coaxialmente a 1m de distância, porém inclinado 30 ° em relação à reta normal a uma coroa circular A 2 . Qual é a irradiação sobre A 1 devido
Considere duas superfícies difusas A 1 e A 2 no interior de uma cavidade esférica com raio R . Usando os métodos a seguir, deduza uma expressão para o fator de forma F 12 em termos de A 2 e R .(a) Det