Um bloco de massa encontra-se parado sobre uma mesa horizontal onde os coeficientes de atrito estático e dinâmico valem, respectivamente, e . Considerando , calcule a intensidade da força que deve ser aplicada paralelamente à mesa, capaz de:
- Fazer o bloco entrar em movimento
- Fazer o bloco se movimentar com velocidade constante (MRU)
Passo 1
Faaaala galerinha, tudo certo? Vamos pra cima dessa questão sobre Atrito!
Bom, o enunciado dá pra gente algumas informações importantes, vamos separá-las aqui:
Show de bola e ele pede pra gente duas coisas
- A força para fazer o bloco entrar em movimento
- A força para o bloco se movimentar com velocidade constante
Vamos analisar as duas opções com calma, então fica tranquilo!
Passo 2
Na letra a) temos a força para fazer o bloco entrar em movimento. Então é o “pré movimento” o auge, a beira (vamos dizer assim) do atrito estático.
Ou seja, temos essa situação aqui:
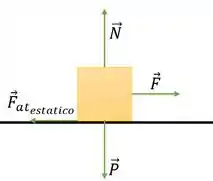
Beleza, para ele estar no pré movimento a força tem que ser igual ao atrito estático máximo.
Então temos que
E a força de atrito estático máximo é dada por
Nesse caso, a Normal é igual ao peso porque o bloco está em um plano horizontal, pois ele não afunda nem flutua. Então, temos que
E o peso vale
A massa e a gravidade são dadas no enunciado, então ficamos com
Beleza, achamos a Normal, colocando isso na fórmula do atrito estático, temos que (lembrado que
Então, como queremos a força mínima para o bloco entrar em movimento, temos que ter essa força um pouquinho maior que essa força de atrito máximo, pois se for igual o bloco vai ficar na iminência do movimento. Vamos escrever dessa forma aqui
Então a força necessária é de
Passo 3
Ufa, vamos agora para letra b)
b) A força para o bloco se movimentar com velocidade constante
Bom, agora estamos falando sobre um bloco em movimento, então usaremos o atrito cinético.
Vamos utilizar a mesma figura só que agora com o atrito cinético, temos que
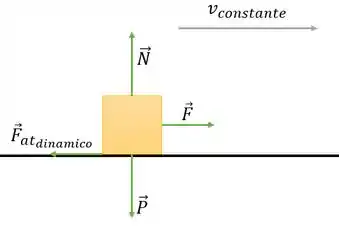
Show, da mesma maneira, temos que
Mas agora estamos falando do bloco em movimento uniforme já que a velocidade é constante, então, pela segunda lei de Newton temos que:
Mas como o movimento é constante, a aceleração é zero, isso implica que
Que é a deixa para que a resultante seja zero também!
O eixo horizontal tem duas componentes com sentidos opostos, vamos considerar o sentido do movimento como referencial, então o vetor que aponta para direita (sentido do referencial) vai ser positivo enquanto o que tem sentido contrario ao referencial vai ser acompanhado pelo sinal negativo! Vamos lá então:
Como vimos, então temos que:
Passando o atrito para o outro lado, temos que
Agora vamos calcular esse !
Do mesmo jeito que o atrito estático, o atrito dinâmico é dado por
Só que ao invés do coeficiente estático, vamos utilizar o dinâmico (faz sentido né?)
Então temos que
E como