Um bloco com massa de está em movimento com aceleração constante na superfície de uma mesa. Sabendo que o coeficiente de atrito dinâmico entre o bloco e a mesa é , calcule a força de atrito entre os dois. Considere .
Passo 1
Faaaaala aí, tudo certinho? Vambora pra mais uma questão sobre atrito!
O enunciado nos dá informações valiosas para seguirmos na nossa jornada, vamos separá-las bonitinho aqui:
E ele quer saber a força de atrito dinâmico (quando o objeto está em movimento)
Passo 2
Show de bolinhas, a primeira coisa que a gente precisa saber é que a força de atrito dinâmico é calculada desse jeitão aqui:
Show de bola, temos o coeficiente de atrito dinâmico mas e a normal?
Passo 3
Bom, como o enunciado diz que ele está sobre uma mesa e não fala nada sobre inclinação vamos considerar um bloquinho assim

Vamos dar uma olhada nas componentes verticais ( o peso e a normal)
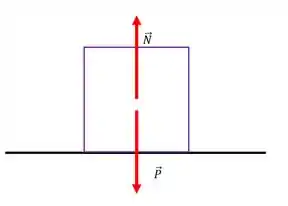
Na vertical, não temos aceleração (senão o objeto ia estar subindo ou afundando no chão) Então a resultante vertical é igual a zero.
E na vertical temos que
Vamos adotar pra cima como o referencial positivo, então tudo que aponta pra cima vai ter o sinal de e o que aponta pra baixo vai ter o sinal de
Pegando os módulos das forças podemos escrever sem as setinhas em cima das letras
Jogando o peso pro outro lado, temos que
Show, o enunciado diz que
Então podemos calcular o peso
Substituindo os valores que temos, ficamos com
Como , então
Passo 4
Segura aí que ainda não acabamos, queremos a força de atrito, lembra que eu te disse que:
Acabamos de achar a normal e temos o valor de
Então