Integral Definida, Substituição Trigonométrica
Um barril com seção reta elíptica está deitado no fundo de um poço cheio de água, com 10 m de profundidade. Ache a força hidrostática exercida sobre a tampa do barril. É dada a equação da elipse nos eixos da figura:
Passo 1
Primeiro passo é entender o que está acontecendo no problema. Um esboço do problema é esse:
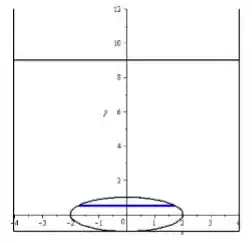
E nessa figura vemos uma projeção do barril no fundo do poço. O que sabemos inicialmente é que cada mini faixa azul do barril sofre ação de uma força hidrostática diferente das demais mini faixas, pois elas são de tamanhos diferentes. Então vamos escrever a força que age sobre cada faixinha de área e que está a uma profundidade em relação ao nível da água.
Passo 2
Agora vamos identificar quanto vale a profundidade em termos de . E sabemos que, como o poço tem 10 metros e de acordo com o esboço que fizemos o nível da água está em , então a profundidade .
Passo 3
Considerando cada minifaixa azul do barril, conseguimos escrever a área de cada minifaixa como . E os valores de e estão relacionados pela equação da elipse dada no problema. Por ela, sabemos que:
Passo 4
E voltando agora pra expressão da força hidrostática, vamos ter:
Integrando a expressão em ambos os lados:
Passo 5
Devemos calcular então:
Fazendo a substituição , teremos que: . E voltando na integral:
Pra resolver essa integral, vamos lembrar de uma identidade trigonométrica que diz que:
E então vamos calcular:
E como , voltando pra variável , temos que:
Avaliando nos extremos do problema:
Passo 6
E agora devemos calcular a outra integral:
Fazendo a substituição , teremos e então reescreveremos a integral assim:
Avaliando nos extremos do problema:
Passo 7
E agora finalmente voltando lá na expressão da força hidrostática, teremos: