Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força hidrostática

Ver Teoria
Exercício 612345

Enunciado

Integral Definida, Integrais Indefinidas

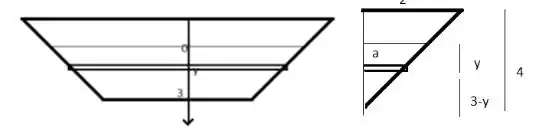
Uma vala está cheia de um líquido de densidade ρ até uma altura de 3 metros. As extremidades da vala são trapézios isósceles com base menor no fundo e medindo 4 metros. A base maior mede 8 metros e a altura do trapézio é de 4 metros. Calcule a força hidrostática em uma extremidade da vala.

Passo 1

Vamos identificar o que foi pedido: Força Hidrostática em uma extremidade da vala! Então vamos escrever a equação que conhecemos de força hidrostática. Sabemos que numa minifaixa de comprimento infinitesimal, como mostrado na figura, a força hidrostática que age sobre essa minifaixa de área d A é:

d F = ρ g y   d A

Só que como a área dessa minifaixa, que é considerada um retângulo de base ( 4 + 2 a ) e altura d y é dada por:

d A = 4 + 2 a d y

Teremos a expressão da força hidrostática nessa minifaixa:

d F = ρ g y 4 + 2 a d y

Passo 2

Reparem que o valor de a é diferente pra cada minifaixa da extremidade da vala. Então temos de achar uma relação entre a e y , pra que a gente possa resolver o problema. E olhando o segundo desenho do enunciado, que mostra só uma lateral da extremidade da vala, podemos utilizar uma semelhança de triângulos e observar que:

2 4 = a 3 - y

a = 3 - y 2

Passo 3

Substituindo o valor de a que encontramos na expressão da força hidrostática, vamos ficar com:

d F = ρ g y 4 + 2 3 - y 2 d y

E agora basta integrar dos dois lados e resolver a seguinte integral:

F = ∫ 0 3 ρ g y 7 - y d y

Resolvendo:

F = ρ g 7 y 2 2 - y 3 3

E avaliando no intervalo [0;3], encontramos:

F = 45 2 ρ g

Resposta

F = 45 2 ρ g     ( N )

Exercícios de Livros Relacionados

Um tanque tem 8 metros de comprimento, 4 de largura e 2 de altura e contém querosene com densidade de 820k g / m 3 até uma profundidade de 1,5 metros. Descubra (a) a pressão hidrostática no fundo do t
Em cada parte, monte, mas não calcule, uma integral que resolva o problema.(a) Encontre a força que um fluido exerce sobre o lado de uma caixa que tem base quadrada com 3 m de lado e está cheia até um
Uma vala é preenchida com um líquido de densidade 840k g / m 3 . As extremidades da vala são triângulos equiláteros com lados de 8m de comprimento e o vértice no fundo. Calcule a força hidrostática em
Um tanque grande é projetado com as extremidades no formato da região entre as curvas y = 1 2 x 2 e y = 12 , medidas em pés. Calcule a força hidrostática em uma extremidade do tanque se ele estiver ch
Um cubo com lados de 20c m de comprimento está no fundo de um aquário no qual a água atinge 1 m de profundidade. Calcule a força hidrostática (a) no topo do cubo e (b) em um dos lados do cubo.