Uma vala é preenchida com um líquido de densidade . As extremidades da vala são triângulos equiláteros com lados de metros de comprimento e o vértice no fundo. Calcule a força hidrostática em uma extremidade da vala.
Passo 1
Primeiramente, vamos entender o problema! O que o enunciado disse pra gente pode ser esboçado mais ou menos assim:
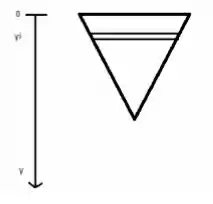
Nessa figura, olhamos a extremidade da vala que é um triângulo equilátero de lado . Se o enunciado pediu a força hidrostática nessa extremidade, vamos escrever a fórmula que nos dá a força hidrostática que age numa faixinha infinitesimal de comprimento , como mostra a figura:
Passo 2
Agora olhando pra faixinha, podemos escrever uma expressão pra área de cada faixinha:
Pois cada faixinha é um retângulo de comprimento e altura .
Passo 3
Olhando agora pra extremidade da vala, que tem a forma triangular, podemos achar uma relação entre e . Ou seja, vamos achar uma relação entre o (medida horizontal da faixinha) que aparece no cálculo da área da faixinha e a profundidade (medida vertical da faixinha). Fazendo uma semelhança de triângulos, podemos dizer que:
Só que como a vala é um triângulo equilátero, a profundidade da vala é a altura do triângulo que é dada por:
E então a relação que encontramos é:
Passo 4
Voltando na expressão da área da faixinha e substituindo a relação encontrada:
E agora vamos substituir essa última expressão na fórmula da força hidrostática:
E essa expressão nos dá a força hidrostática em uma faixnha da extremidade da vala. Então se somarmos todos esses de todas as faixinhas, vamos obter a força que age na extremidade da vala. Então somando na direção , de até :
Passo 5
A integral acima é equivalente a: