Calcule a máxima velocidade terminal em uma amostra de partículas de sílica, com diâmetros entre e , sedimentando em água à . Considere que a concentração de partículas no fluido é muito baixa.
Dados: e
Passo 1
Temos uma amostra de sílica com diâmetros que variam de a mas que possui esfericidade constante (). O problema pede a máxima velocidade terminal nessa amostra.
O fluido em que as partículas estão sedimentando é água à . Repara que eu não dei dados sobre o fluido no enunciado e isso foi proposital. Na prova, nem sempre você vai ter esses dados diretamente; muitas vezes vai ser que nem nesse enunciado aqui: só diz o fluido e a temperatura dele. Aí, vamos ter que ir atrás de tabelas relacionando temperatura, densidade e viscosidade dinâmica (que é o ) para o fluido em questão. Indo numa dessas tabelas, você vai achar que:
Outro ponto do enunciado que vale a pena ressaltar é quando fala “Considere que a concentração de partículas no fluido é muito baixa.”, que, basicamente, é dizer que não precisa fazer correção de concentração para a velocidade terminal.
Passo 2
Temos que, antes de qualquer coisa, determinar qual é o diâmetro da faixa que tem maior velocidade terminal. Dá uma olhada na fórmula “genérica” de velocidade terminal:
Tanto a área projetada como o volume podem ser escritos como uma constante (que depende da morfologia da partícula) vezes uma potência do diâmetro. Para o volume, essa constante é o fator de forma ; para a área projetada, não tem nenhuma constante específica, então bora dizer que essa constante é .
Daí, simplificando os diâmetros:
Bora comparar as velocidades terminais de duas partículas, e , dessa amostra com . Não sei se as velocidades são=, ou , daí vou usar uma interrogação entre elas:
Tudo que for constante e igual dos dois lados a gente pode cortar.
- Como as partículas possuem mesma morfologia (lembra que essa é uma premissa que sempre usamos para partículas de um mesmo material mesmo se o enunciado não explicitar isso, mas, nesse caso, ele deixou implícito quando deu uma esfericidade só): e .
- Estando as partículas no mesmo fluido, estamos com iguais
- Como estão todas as partículas juntas submetidas a um único campo de forças, é um só
- Como as partículas são do mesmo material, é um só
Daí:
Vimos, lá na teoria, que depende de e , isto é, . Como a morfologia é igual nos dois casos, sobra apenas pra analisar. A fórmula do é
Ou seja, quanto maior , maior o . Agora, lembra lá daquele gráfico :
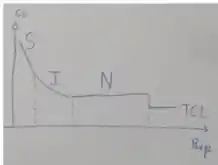
Conforme o aumenta, ou diminuiu ou fica constante, mas nunca aumenta.
- Se :
- Se :
Como :
Daí:
Daí:
Ou seja, a velocidade terminal é sempre maior quanto maior for o diâmetro da partícula, comparando-se partículas de mesmo material e nas mesmas condições. Isso é uma coisa que você tem que saber. Eu demonstrei matematicamente aqui, mas na prova, muito provavelmente, você não vai precisar. Basta lembrar.
Voltando, temos que ver qual é o maior diâmetro da amostra pois é pra ele que temos que calcular a velocidade terminal. E ele é:
Passo 3
Não sabemos qual o regime de escoamento e não queremos ficar iterando então vamos aplicar as correlações de Coelho e Massarani, mas qual caminho seguir, ou ?
Repara que nós temos e ,mas queremos . Daí, vamos por :
Repara que eu joguei todos os valores na fórmula com unidades do CGS (centímetro-grama-segundo). Não podemos misturar sistemas de unidades, hein! Cuidado com isso! Lembrando que o Poise é a unidade de viscosidade dinâmica do CGS.
Como fomos por , para calcular o usamos:
Opa! Não sabemos e . Bora calcular:
Daí:
Usando a definição de :