1. Determinar, pela extrapolação de dados, a velocidade terminal das partículas à diluição infinita e, a partir deste valor, calcular o diâmetro das partículas

Lá no passo 1, disse que extrapolação é ver a tendência dos pontos e assumir que eles vão continuar essa mesma tendência até chegar onde queremos analisar. E a melhor forma de ver essa tendência é jogando os pontos num gráfico:



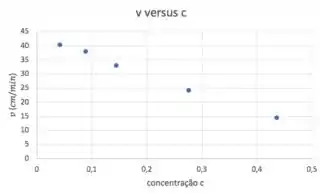
Repara que esses pontos estão mais ou menos alinhados em uma reta, certo? Se você estivesse numa prova (provavelmente estaria fazendo esse gráfico em papel milimetrado), teria que pegar uma régua e traçar a melhor reta para esses pontos. Tipo assim:



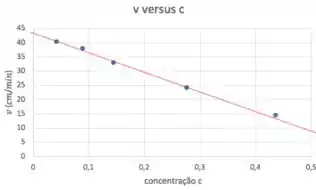
Agora, é só ver, para , qual o valor de Eu diria uns . E não se estressa se você tiver dito , por exemplo. Método gráfico tem muita incerteza mesmo. Só não pode ter dito , por exemplo.

Uma parte já foi, temos . Agora, ainda falta calcular Repara que:

E não temos , daí não podemos calcular e aí não sabemos em qual região estamos (Stokes, Intermediária, Newton ou TCL). Dessa forma, não sabemos qual fórmula usar pra .

Para fugir de iterações, vamos usar as correlações de Coelho e Massarani.

“Ixi, Marcelo! Não lembro quando usar ou usar .” Relaxaaa. Uma dica que eu dou é olhar pro formulário, ver a cara dessas duas expressões e ver as informações que você tem. Olha só:

Para calcular , precisamos de , que é justamente o que não sabemos e queremos calcular. Daí NÃO é essa que vou usar. Mas olha pra agora; temos tudinho : )

Massssss, temos que lançar na fórmula tudo no mesmo sistema de unidades (SI, CGS, sistema inglês etc) pra ser dimensionalmente consistente né. Embora eu adore o SI, aqui na parte de operações unitárias que envolve partículas, na maioria das vezes, é bem conveniente usar o CGS, então vai ser o que você mais vai me ver usando. Bora reunir tudo, convertendo o precisar pro CGS (centímetro-grama-segundo):

Daí:

Agora, obtemos por outra correlação de Coelho e Massarani:

Mas antes precisamos calcular e , sabendo que o enunciado deu :

Substituindo:

Agora sim podemos ir pra definição de , porque só vai sobrar uma variável:

Passo 3

2. Comparar os resultados experimentais com as estimativas segundo a correlação empírica de Richardson & Zaki.

A correlação empírica de Richardson & Zaki é:

Em que o valor de do é calculado de forma diferente dependendo do :

Sendo o Reynolds calculado supondo que a esfera está isolada.

Bora pras contas que vãos entender melhor como usar isso tudo. Vou usar o ponto (.

Precisamos de , que é a concentração volumétrica:

Mas temos uma concentração em massa por volume:

Pra converter, bora adotar uma base de cálculo de de suspensão, que vai ter uma massa de partículas, por regra de três:

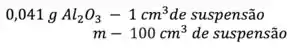
Podemos obter o volume dessa massa já que nos foi dada a densidade das partículas, .

Jogando na fórmula de :

E a velocidade terminal associada a essa concentração é , que é o nosso .

Precisamos do pra continuar e, lá na teoria, eu disse que ele é o Reynolds calculado supondo que a esfera está isolada, ou seja, pega esse e finge que a esfera que tem essa velocidade está isolada, mesmo sabendo que, na verdade, ela NÃO está. Daí, vamos usar o como se ele fosse o . Mas antes, precisamos passar pro CGS, que é o sistema que estamos usando:

Agora sim, com essa velocidade:

Agora, calculando o :

Repara que e NÃO mudaram porque a esfericidade ainda é a mesma.

Como , calculamos por

Daí, calculando , que é a velocidade que relacionaremos, depois, com o tamanho da partícula:

Essa velocidade é um pouquinho diferente da que “achamos” pela extrapolação, que era .

Vamos, agora, calcular o diâmetro da partícula. Vamos, para isso, usar o , que é o associado com esse movimento nessas condições do problema.

Como o enunciado fala para comparar “oS resultadoS”, acho que ele tava querendo que fizéssemos isso para todos os pontos e depois tirássemos uma média dos resultados. Mas ao invés de ficar repetindo várias e várias vezes a mesma coisa, mecanicamente, acho que podemos aproveitar melhor nosso tempo vendo coisas diferentes. Então bora continuar.