Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Formas Quadráticas – Cônicas

Ver Teoria
Exercício 612345789

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.8

Considere as seguintes afirmações:

I . A imagem da curva γ 1 ( t ) = ( c o s ( 2 t ) , s i n 2 ( t ) ) , t ∈ ℝ está contida em uma reta.

I I . A imagem da curva γ 2 ( t ) = ( e 2 t , e t ) , t ∈ ℝ é uma parábola.

I I I . A imagem da curva γ 3 ( t ) = ( e t + e - t , e t - e - t ) , t ∈ ℝ está contida em uma hipérbole.

São corretas apenas as afirmações

a .   I ;   b .   I I ;   c .   I I I ;   d .   I   e   I I I ;   e .   I I   e   I I I .

Passo 1

Eaew, tudo bem?

Temos que considerar as afirmações

I . A imagem da curva γ 1 ( t ) = ( c o s ( 2 t ) , s i n 2 ( t ) ) , t ∈ ℝ está contida em uma reta.

I I . A imagem da curva γ 2 ( t ) = ( e 2 t , e t ) , t ∈ ℝ é uma parábola.

I I I . A imagem da curva γ 3 ( t ) = ( e t + e - t , e t - e - t ) , t ∈ ℝ está contida em uma hipérbole.

e, então escolher a alternativa que afirma corretamente a veracidade dos três itens. Vamos analisar cada caso tendo em vista o gráfico e a estrutura da parametrização! Saca só!

Passo 2

A primeira afirmativa é tal que

I . A imagem da curva γ 1 ( t ) = ( c o s ( 2 t ) , s i n 2 ( t ) ) , t ∈ ℝ está contida em uma reta.

podemos verificar essa afirmação analisando a derivada da curva, temos que

γ ' 1 ( t ) = d d t [ c o s ( 2 t ) , s i n 2 ( t ) ] = [ - 2   s i n ( 2 t ) , 2 s i n ( t ) c o s ( t ) ]

se a curva for uma reta, temos que a inclinação da reta tangente será independente de ponto, como a definição de inclinação da reta tangente é tal que

m = d x / d t d y / d t = - 2   s i n ( 2 t ) 2   s i n ( t ) c o s ( t )

como temos que

s i n ( 2 t ) = 2   s i n ( t ) c o s ( t )

podemos simplificar a nossa inclinação

m = - 2

note que ela é constante para todo t , ou seja, essa parametrização é uma reta! Para reforçar, observe o gráfico

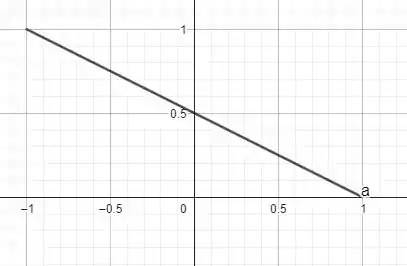
Afirmação I é verdadeira! Vamos para a próxima!

Passo 3

A segunda afirmação é tal que

I I . A imagem da curva γ 2 ( t ) = ( e 2 t , e t ) , t ∈ ℝ é uma parábola.

Vamos tentar escrever essa parametrização no formato de uma parábola, ou seja, uma relação quadrática entre os dois termos, será que isso é possível? A primeira vista é, note que se

x = e t → y = x 2 = e 2 t

Mas note que se tomarmos o logaritmo em ambos os lados das expressões, temos que

l n ( x ) = t e l n ( y ) = 2 t

de forma que a nossa “parábola” só é bem definida para x > 0 e y > 0 , ou seja, apenas o primeiro quadrante, sendo assim, ela é somente meia-parábola e não uma parábola completa! O gráfico é tal que

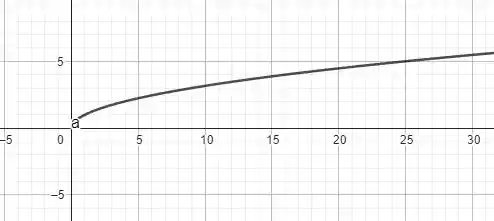
A afirmativa I I é falsa! Vamos para a última agora!

Passo 4

Por último temos que verificar se

I I I . A imagem da curva γ 3 ( t ) = ( e t + e - t , e t - e - t ) , t ∈ ℝ está contida em uma hipérbole.

Note que cada componente desta curva é definido em termos das identificações

c o s h ( t ) = e t + e - t 2 e s e n h ( t ) = e t - e - t 2

de forma que

γ 3 ( t ) = ( 2   c o s h ( t ) , 2   s e n h ( t ) )

que é parametrização de uma hipérbole com vértices em ± 2 . O gráfico é dado por

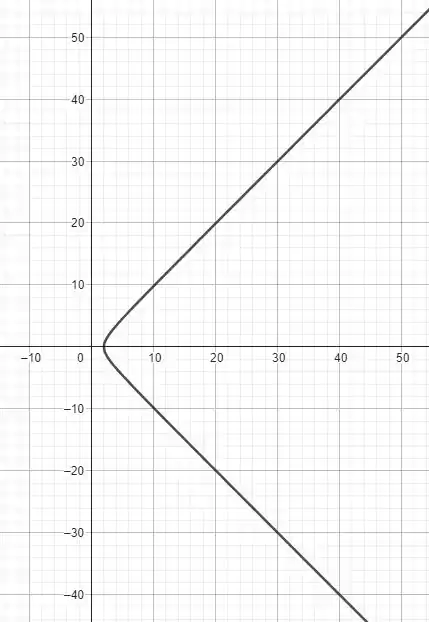
A afirmação I I I é verdadeira! Portanto, a alternativa verdadeira é a d . A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

Alternativa d .   I   e   I I I .

Exercícios de Livros Relacionados

Simplifique a equação dada por uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos. 3 x 2 - 3 x y - y 2 - 6 y = 0
Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região limitada pela hiperbole x 2 / a 2 - y 2 / b 2 = 1 e pela reta x = 2 a
No exercício, (a) ache a excentricidade, os focos e as diretrizes da cônica central dada. (b) faça um esboço mostrando a cônica, os focos e as diretrizes. 25 x 2 - 9 y 2 = 225
Uma corda focal de uma cônica é divvida em dois segmentos pelo foco. Prove que a soma dos recíprocos das medidas dos comprimentos dos dois segmentos é a mesma, não imporá a corda tomada.
Ache a equação polar da parábola contendo o ponto ( 2 ,1 3 π ), cujo foco está na origem e cujo vértice está na extensão do eixo polar.