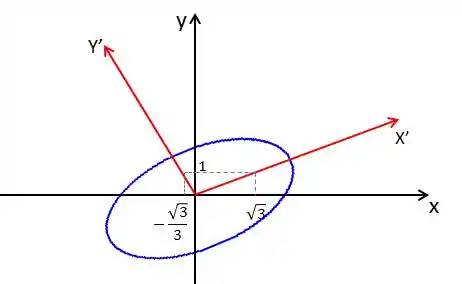
Efetue uma rotação nos eixos coordenados a fim de eliminar o termo . Identifique a cônica e escreva sua equação no sistema obtido após a rotação. Esboçar o gráfico
Passo 1
Essa cônica não está na forma que costumamos ver. Vamos escrever a forma matricial dela.
Passo 2
Agora temos que encontrar os autovalores de .
Bom, para encontrar os autovalores de uma matriz 2x2 fazemos o seguinte:
Precisamos fazer:
Isso implica :
Montamos um polinômio característico e resolvemos. Os valores encontrados vão ser os autovalores. Vou mostrar:
No caso, a nossa matriz é:
O polinômio característico vai ser:
Resolvendo essa equação, achamos os autovalores de , que são e
Passo 3
Agora, temos de encontrar os autovetores unitários.
Para uma matriz 2x2:
Com autovalores e vamos encontrar autovetores associados a cada autovalor.
No nosso caso:
Autovetor associado a :
Com
A expressão matricial fica:
Fazendo a multiplicação matricial temos o seguinte sistema:
Temos:
Portanto
Arbitrando um valor qualquer para , por exemplo temos:
Porém necessitamos do autovetor unitário. Fazemos então:
Passo 4
Autovetor associado a :
Com
A expressão matricial fica:
Fazendo a multiplicação matricial temos o seguinte sistema:
Temos:
Portanto
Arbitrando um valor qualquer para , por exemplo temos:
Porém necessitamos do autovetor unitário. Fazemos então:
Passo 5
Então, reescrevendo a equação temos:
E multiplicando as matrizes, chegamos em:
Ajeitando:
Que é a equação de uma elipse.
Passo 6
Seu gráfico é uma elipse rotacionada:
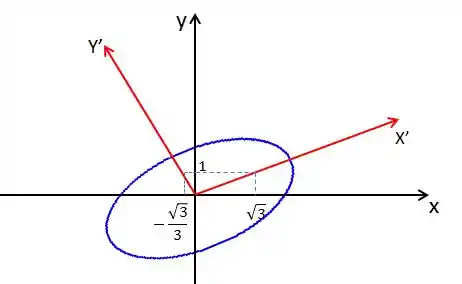
Resposta
É uma elipse. Seu gráfico é: