Abaixo é mostrado um eixo maciço e circular de diâmetro 200mm de uma barra de aço. Essa barra possui . Sabendo disso e ainda que há uma carga de 10 KN que contribui na torção, determine o valor máximo de sem que haja rompimento da barra. Analise apenas as contribuições referentes aos esforços torsores.
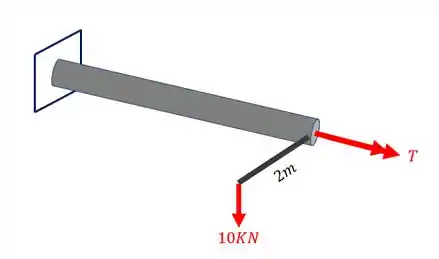
Passo 1
Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do torque máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula
Porém também sabemos que queremos o torque máximo, e para termos o torque máximo devemos fazer pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.
Passo 2
Outra coisa que precisamos calcular é o nosso momento polar de inercia (). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação
Substituindo na nossa equação principal, teremos que
Passo 3
O que precisamos saber agora é que queremos o valor máximo do nosso torque sem que haja rompimento. Para garantirmos isso devemos fazer
Agora a única coisa que falta é determinarmos o torsor máximo que está atuando na nossa peça.
Passo 4
Para determinar o torsor devemos tomar alguns cuidados. O primeiro é que temos duas contribuições para os nossos torsores. Uma é o próprio T máximo que queremos determinar, a outra é a carga de 10 KN que produzirá o torsor mostrado na figura abaixo.
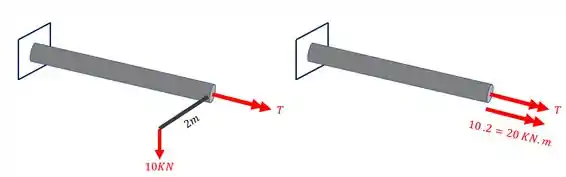
Logo podemos definir o nosso torsor como
Passo 5
Vamos resolver a nossa fórmula então
Sabemos que
E o torque deixamos para calcular por último.
Substituindo teremos que
Isolando o valor de T teremos que
Mas devemos lembrar que
Como acabamos de descobrir o valor do torque que podemos aplicar ao todo, basta descobrirmos qual o valor do torque parcial que podemos aplicar.
Substituindo teremos que
Logo contando com os torsores aplicados, o maior torque que poderia ser dado nessa peça seria de 105,7 KN.m.