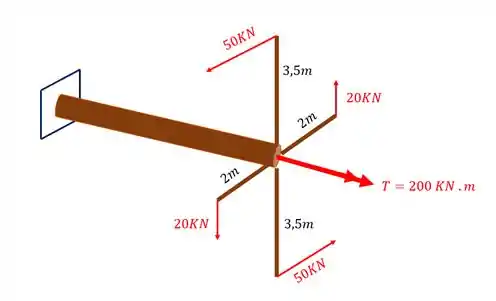
A barra de madeira abaixo representa o eixo de giro de um moinho. Por problemas nas engrenagens uma das extremidades do eixo ficou presa. Sabendo que o eixo foi sujeito aos esforços torsores mostrados abaixo e que a resistência ao cisalhamento dessa barra (levando em consideração apenas esforços torsores) é de 25 Mpa, determine o raio máximo que a nossa barra poderá ter para que o eixo não rompa.
Passo 1
Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do raio máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula
Porém também sabemos que queremos o torque máximo, e para termos o torque máximo devemos fazer pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.
Passo 2
Outra coisa que precisamos calcular é o nosso momento polar de inercia (). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação
Substituindo na nossa equação principal, teremos que
Passo 3
O que precisamos saber agora é que queremos o valor máximo do nosso raio sem que haja rompimento. Para garantirmos isso devemos fazer
Agora a única coisa que falta é determinarmos o torsor que está atuando na nossa peça.
Passo 4
Para determinarmos o torsor que está agindo na nossa peça, vamos ir trocando cada braço de alavanca pela ação de um torsor ligado a ele, com isso teremos que
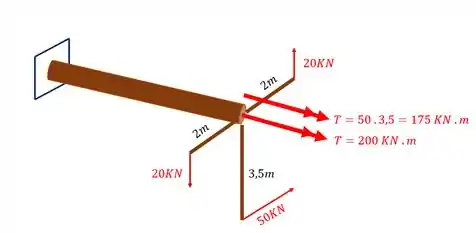
Podemos ver que a barra de baixo dará a mesma contribuição da barra de cima
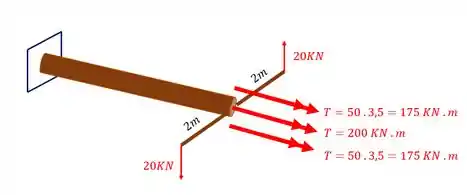
Colocando também as contribuições laterais teremos que
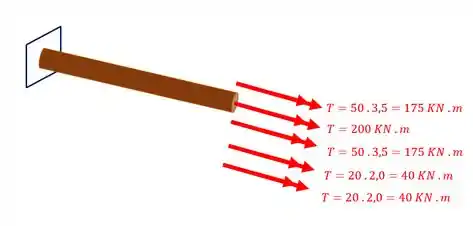
Logo podemos definir o nosso torsor como
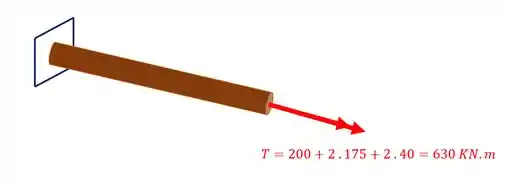
Passo 5
Vamos resolver a nossa fórmula então
Sabemos que
Substituindo teremos que
Isolando o valor de T teremos que