Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fórmula da Torção

Ver Teoria
Exercício 81234567

Enunciado

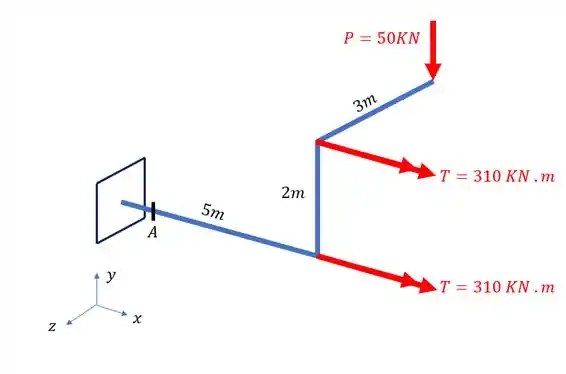
Na figura baixo temos desenhado uma estrutura sujeita a três carregamentos, uma carga de 5 0   K N e dois torques de 31 0   K N . m . Considerando apenas os efeitos do esforço torsor, determine o valor do cisalhante máximo que ocorre no ponto A da nossa barra.

t o d o s   o s   e i x o s   s ã o   f u r a d o s   e   c i r c u l a r e s    

r i n t e r n o = 50 c m

r e x t e r n o = 80 c m

Passo 1

Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do cisalhante máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula

τ = T   .   ρ J

Porém também sabemos que queremos o cisalhante máximo, e para termos o cisalhante máximo devemos fazer ρ = r e x t e r n o pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.

τ m á x = T   . r e x t e r n o J

Passo 2

Outra coisa que precisamos calcular é o nosso momento polar de inercia ( J ). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação

J = π . ( r e x t e r n o 4 - ( r i n t e r n o ) 4 )   2

Substituindo na nossa equação principal, teremos que

τ m á x = T   . r e x t e r n o J

τ m á x = T   . r e x t e r n o π . ( r e x t e r n o 4 - ( r i n t e r n o ) 4 )   2

τ m á x = 2 . T . r e x t e r n o π . ( r e x t e r n o 4 - ( r i n t e r n o ) 4 )

Passo 3

O raio definimos facilmente, porém devemos tomar cuidado com o torsor, pois esse se trata do torsor máximo que está agindo na nossa peça, para descobrirmos o seu valor faremos a seguinte sequência de passos.

Primeiro cortamos a nossa barra no ponto que desejamos calcular o torsor

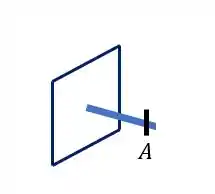
Em seguida levamos até essa seção todos os esforços que tínhamos antes de cortar e que após o corte não estamos vendo mais. Como só nos interessa analisar efeitos do torsor, podemos levar os nossos 2 torques de 31 0   K N   . m diretamente para seção.

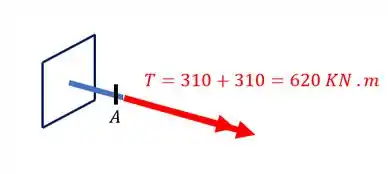
Também temos que levar os esforços torsores causados pela carga de 5 0   K N . Para calcular o seu valor precisamos analisar o seu braço de alavanca, olhando a figura abaixo teremos que

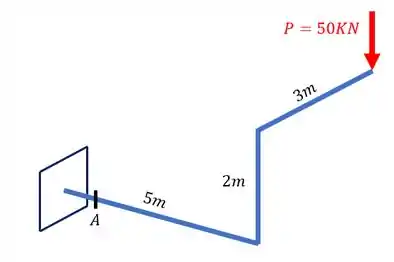
Trocando a nossa carga pelo efeito torsor causado por ela teremos que

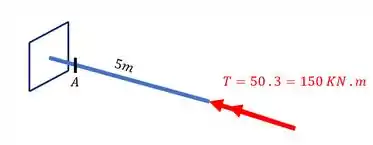
Levando esse esforço para nossa seção A teremos que

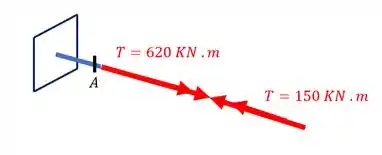
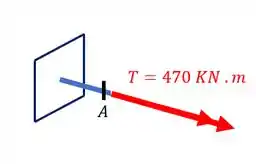
Logo também já temos o nosso torsor que age na peça que é dado por

T = 47 0   K N . m

Passo 4

Agora que já temos tudo que precisamos, basta substituir e determinar o valor do nosso cisalhante máximo

τ m á x = 2 . T . r e x t e r n o π . ( r e x t e r n o 4 - ( r i n t e r n o ) 4 )

T = 47 0   K N . m

r i n t e r n o = 50 c m = 0,50 m

r e x t e r n o = 80 c m = 0,80 m

Substituindo teremos que

τ m á x = 2   .   470   .   0,80 π . ( 0,80 4 - 0,50 ) 4 ) = 689,6 K N m 2 = 689,6   K P a

Resposta

τ m á x = 689,6   K P a

Exercícios de Livros Relacionados

Sob condições normais de operação. um motor exerce um torque de intensidade T F = 1200 lb ⋅ in. em F, Sabendo que r D = 8 in., r G =3 in. e que a tensão de cisalhamento admissível é 10,5 ksi em cada e
Sob condições normais de operações.um motor exerce um torque de intensidade T, em F. Os eixos são feitos de aço para qual tensão de cisalhamento admissível é de 12 ksi e têm diâmetro d C D E = 0,900 i
Os eixos do conjunto de polias mostrado na figura devem ser redimensionados. Sabendo que a tensão de cisalhamento admissível em cada eixo é de 58,6 MPa, determine o menor diâmetro admissível para (a)
(a) Para uma dada tensão de cisalhamento admissível, determine a relação T / w do torque T máximo admissível e o peso da unidade de comprimento w para o eixo vazado mostrado na figura. (b) Chamado de
Um torque T de 5k i p * pés é aplicado a um eixo de alumínio de seção vazada com sua seção transversal mostrada na figura. Desprezando o efeito da concentração de tensões, determine a tensão de cisalh