O sistema da figura é constituído por um eixo de seção transversal cheia e com uma tensão de cisalhamento admissível de , e por um tubo feito de latão com uma tensão de cisalhamento admissível de .
Determine o maior torque que pode ser aplicado em , sem que a tensão de cisalhamento admissível do material do tubo seja excedida e o valor correspondente necessário para o diâmetro do eixo .
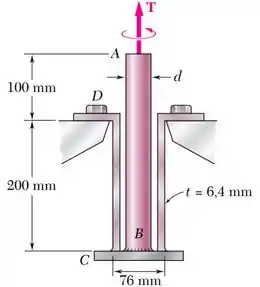
Passo 1
O que está acontecendo?
O eixo maciço possui uma tensão de cisalhamento admissível e um raio , onde é o seu diâmetro.
Já o tubo tem:
- Uma tensão de cisalhamento admissível ;
- Um diâmetro externo de , e, consequentemente, um raio externo ;
- Uma espessura ;
- E um raio interno .
Eles estão submetidos a um torque .
E o que é que o exercício quer?
No item , ele quer saber o maior torque que pode ser aplicado sem que a tensão de cisalhamento do tubo seja excedida.
Ou seja, ele quer saber o maior torque que ainda gera, no tubo , uma tensão máxima que satisfaça a condição:
Então podemos usar essa condição e desenvolvê-la usando a fórmula da torção () para encontrar o torque máximo .
Já no item , ele quer saber o diâmetro necessário para o eixo para que ele suporte o torque encontrado no item anterior.
Para encontrar esse diâmetro, vamos aplicar a mesma condição que usamos com o tubo para o eixo :
Mas dessa vez, vamos desenvolver essa condição com o objetivo de encontrar o diâmetro mínimo.
Passo 2
Vamos começar resolvendo o item !
Para o tubo , temos que:
Aqui, a tensão máxima pode ser descrita pela fórmula da torção:
No caso do tubo , definimos o raio externo como .
Então a fórmula da torção aplicada para o tubo fica assim:
Substituindo isso na condição de projeto, temos que:
E isolando o torque aplicado , encontramos que:
Além disso, para o tubo , que possui um raio interno e um raio externo , o momento de inércia polar vai ser dado pela fórmula:
Dessa forma, a nossa expressão anterior fica assim:
Finalmente, substituindo os valores:
- ;
- ;
- & ,
Encontramos que:
Como esse número é muito grande, reescrevemos ele em :
Ou seja, o maior torque que pode ser aplicado em , sem que a tensão de cisalhamento admissível do material do tubo seja excedida, é:
Passo 3
Agora, resolvemos o item .
Para o eixo maciço , temos que:
Agora, aplicando a fórmula da torção para o eixo , temos que:
Dessa forma, a nossa condição anterior fica assim:
Aqui, temos que o momento polar de inércia do eixo maciço de raio vai ser dado pela fórmula:
Então podemos substituir isso na nossa expressão anterior para encontrar que:
Arrumando tudo, isso fica assim:
E, aqui, ainda podemos fazer mais uma substituição, que é a de que o raio do eixo é igual à metade do seu diâmetro .
Fazendo isso, temos que:
E, mais uma vez, arrumando tudo, temos:
Como queremos encontrar o diâmetro mínimo, devemos isolá-lo:
Espelhando essa expressão e fazendo a raiz cúbica, temos que:
Finalmente, substituindo:
- ;
- ,
Encontramos que:
Ou seja, o valor necessário para o diâmetro do eixo correspondente ao torque encontrado no item é:
E assim terminamos o exercício!