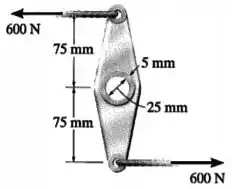
O elo funciona como parte do controle do elevador de um pequeno avião. Se o tubo de alumínio conectado tiver de diâmetro interno e parede de de espessura, determine a tensão de cisalhamento máxima no tubo quando a força de for aplicada aos cabos. Além disso, trace um rascunho da distribuição da tensão de cisalhamento na seção transversal.
Passo 1
O que está acontecendo?
As forças geram, com braços , um torque de sentido anti-horário () no tubo vazado de alumínio.
Esse tubo tem um diâmetro interno e uma espessura de .
Com isso, conseguimos concluir que:
1. O tubo tem um diâmetro externo , e, consequentemente, um raio externo :
& 2. O tubo tem um raio interno :
E o que é que o exercício quer saber?
Ele quer que a gente calcule a tensão de cisalhamento máxima no tubo quando as forças são aplicadas.
Para calcular essa tensão máxima, vamos usar a fórmula da torção:
Onde:
- é o torque resultante gerado pelas forças aplicadas;
- & é o momento de inércia polar do tubo vazado, que vai ser dado pela fórmula:
Além de tudo isso, o exercício também quer que a gente esboce a distribuição da tensão de cisalhamento na seção transversal do tubo.
Passo 2
Vamos começar pelo cálculo do torque resultante no tubo.
Esse torque vai ser o somatório dos torques causados por cada força .
E como essas forças possuem um braço , o torque causado por elas vai ser igual à .
Sendo assim, vamos ter que:
O que significa que:
Passo 3
Calculado o torque resultante no tubo, podemos seguir para o cálculo da tensão de cisalhamento máxima .
Para tanto, aplicamos a fórmula da torção:
Substituindo a expressão encontrada no Passo 2 para e a fórmula indicada no Passo 1 para , temos que:
E, arrumando tudo, isso fica assim:
Com isso, só falta substituir os valores:
- ;
- ;
- ;
- & ,
Para encontrarmos que:
Substituindo por e fornecendo o resultado final com três algarismos significativos, temos que:
Passo 4
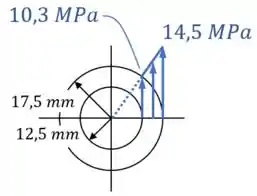
Por último, para finalizar o exercício, vamos fazer o esboço da distribuição da tensão de cisalhamento na seção transversal do tubo.
Sabendo que essa distribuição varia linearmente:
- Desde no ponto central do tubo;
- Até na superfície externa do tubo,
Esse esboço fica assim:
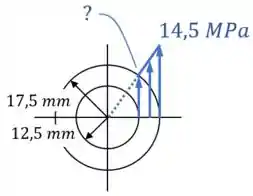
Agora, esse esboço está incompleto porque a gente não sabe qual o valor da tensão na superfície interna do tubo vazado.
Para calcular a tensão em uma região de raio de um eixo, podemos usar a fórmula:
(Lembra? Essa fórmula pode ser obtida combinando as fórmulas e .)
Substituindo , e , conseguimos definir o valor da tensão na superfície interna:
Dessa forma, o nosso esboço final fica assim: