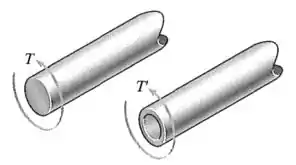
Um eixo é feito de aço com tensão de cisalhamento admissível . Se o diâmetro do eixo for , determine o torque máximo que pode ser transmitido. Qual seria o torque máximo se fosse feito um furo de de diâmetro no eixo? Faça um rascunho da distribuição da tensão de cisalhamento ao longo de uma linha radial em cada caso.
Passo 1
O que está acontecendo?
O exercício quer que a gente estude dois eixos com um diâmetro de : um maciço e um vazado, com um diâmetro interno de .
Sendo assim, esses eixos vão ter:
Um raio externo ;
E um raio interno , no caso do eixo vazado.
E o que é que o exercício quer?
Ele quer saber qual são os torques máximos e que podem ser transmitidos pelos eixos maciço e vazado, respectivamente.
Esses torques máximos vão ser os torques que vão gerar, de acordo com a fórmula da torção...
...uma tensão de cisalhamento nos eixos igual à tensão de cisalhamento admissível .
Dessa forma, podemos aplicar as condições...
...e desenvolver essas expressões para encontrar os torques máximos e .
Além disso, o exercício ainda quer que a gente esboce a distribuição da tensão de cisalhamento ao longo de uma linha radial em cada eixo.
Passo 2
Vamos começar pelo cálculo do torque máximo no eixo maciço.
Começamos aplicando a condição:
E substituindo a fórmula da torção:
Em seguida, isolamos para encontrar que:
Agora, para calcular o torque máximo , vamos ter que conhecer o momento de inércia polar da seção transversal do nosso eixo.
Então lembra aí!
Para um eixo maciço de raio , a fórmula desse momento de inércia polar é:
Com isso, o nosso torque máximo fica assim:
Simplificando tudo, encontramos que:
Finalmente, substituindo:
;
& ,
temos que:
O que dá:
Como esse resultado é muito grande, podemos reescrevê-lo em :
Passo 3
Em seguida, vamos fazer o cálculo do torque máximo no eixo vazado.
Mais uma vez, começamos aplicando a condição:
E substituindo a fórmula da torção:
Isolando , encontramos que:
E... Lembra aí!
O momento de inércia polar de um eixo vazado de raio externo e raio interno é dado pela fórmula:
Dessa forma, o nosso torque máximo fica assim:
E, simplificando tudo, isso fica assim:
Finalmente, substituindo:
;
;
& ,
encontramos que:
Como esse resultado é muito grande, podemos reescrevê-lo em :
Passo 4
Por fim, vamos esboçar as distribuições da tensão de cisalhamento ao longo de uma linha radial em cada eixo.
Então vamos nos lembrar do que vimos na teoria...
Essa distribuição é linear, variando desde no centro dos eixos até (que vai ser igual à nos nossos casos) na superfície externa dos eixos:

Agora, para completar esses esboços, só precisamos calcular qual é a tensão na superfície interna do eixo vazado.
Para isso, usamos a fórmula da torção em sua versão geral, que fornece a tensão em um ponto distante um raio do centro do eixo:
No nosso caso, queremos saber a tensão na superfície interna do eixo vazado, onde , e temos que .
Então essa fórmula fica assim:
Por fim, substituindo:
;
;
& ,
encontramos que:
Com isso, os nossos esboços ficam assim:

E assim terminamos o exercício!