O eixo suporta as cargas das duas polias mostradas na figura. Determine a equação da linha elática. Os mancais em e exercem somente reações verticais sobre o eixo. constante.
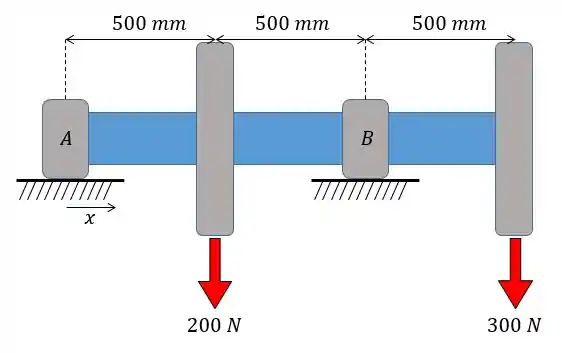
Passo 1
Bom pessoal vamos aplicar o que vimos na teoria e achar o momento fletor utilizando as equações de descontinuidade, para depois aplicarmos a equação da linha elástica:
A primeira coisa que temos de fazer é achar todas as forças atuantes na barra, então temos de achar as reações nos apoios. Feito isso vamos colocar tudo em função de cargas e integrar duas vezes para achar o momento fletor.
Passo 2
Vamos achar as reações nos apoios, para isso a gente vai fazer um desenho das forças:
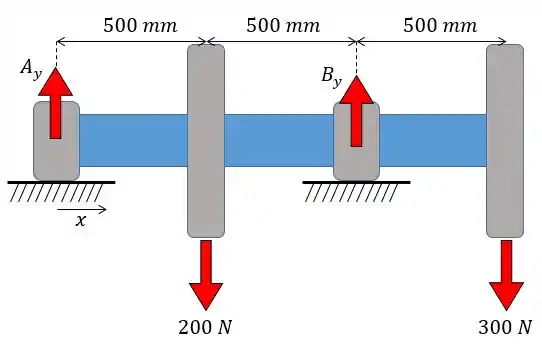
Agora vamos ser bem malandrinhos e aplicar primeiro o equilíbrio dos momentos em relação ao ponto :
E portanto,
Passo 3
Agora temos que colocar as forças como funções de . Vamos olhar o desenho novamente:
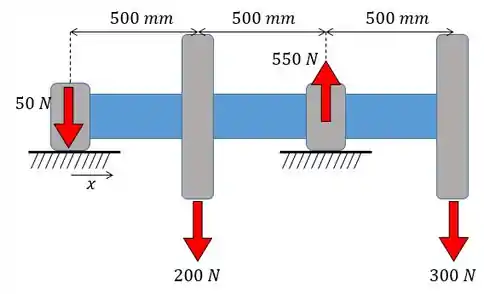
As forças aparecem como:
Pessoal, aqui (e em qualquer outro exercício) não faz diferença colocar ou não a última força. Isso porque nunca vai ser maior do que o último ponto, portanto se a última força estiver na extremidade ela não faz mais diferença no problema.
Passo 4
Agora é só integrar uma vez para achar a força cortante.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
Ficou bem grandinho né? haha
Mas é tranquilo, vem comigo!!
E agora para achar o momento fletor é só integrar novamente.
Pronto! temos a nossa resposta do problema!
Ajuda muito não é mesmo? Não precisamos fazer um momento de desenhos e cálculos...
Passo 5
Como o problema pediu a linhas elástica então a gente deve aplicar a função do momento que encontramos na equação da linha elástica:
Podemos escrever da seguinte forma:
Substituindo:
Vamos integrar a primeira vez:
Agora podemos integrar novamente:
E pronto, achamos a nossa equação da linha elástica mas ainda falta achar as constantes e .
Passo 6
Para achar as constantes a gente só precisa lembrar que os mancais impedem a deflexão, portanto tanto em quanto nós vamos ter . Sendo assim, podemos substituir:
Para nós vamos ter:
Lembre-se que vários termos zeraram porque estamos falando de uma função de descontinuidade, logo os termos e vão zerar!
Para nós vamos ter:
Com isso a nossa equação da linha elástica fica da forma: