A viga está sujeita à carga mostrada na figura. Determine as equações da inclinação e da linha elástica. é constante.
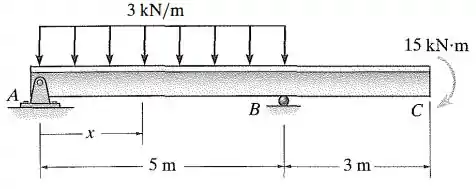
Passo 1
Galera essa questão já começa a misturar os tópicos de função de descontinuidade com linha elástica. Então vamos lembrar que o cálculo da linha elástica é feito como:
A gente pode escrever ainda uma equação da linha elástica diretamente com a carga:
Então nós vamos achar a linha elástica utilizando esse tipo de função! Partiu?
Passo 2
Vamos começar achando as reações nos apoios, para isso a gente vai fazer um desenho das forças:
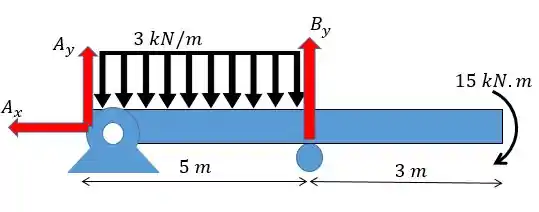
Como só existe uma força no eixo então vamos ter que:
Fazendo o somatório de forças no eixo :
A força exercida pela carregamento uniforme é dada por:
Substituindo na equação:
Agora vamos aplicar o somatório dos momentos em relação ao ponto considerando o sentido anti-horário como positivo:
Lembrando que o ponto de atuação da força exercida pelo carregamento uniforme se encontra na metade do carregamento. Fica assim:
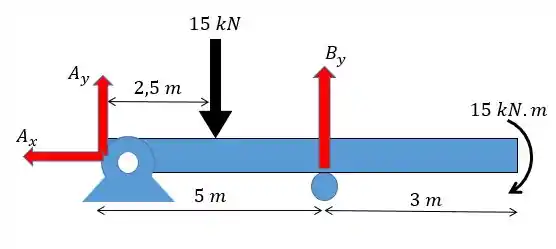
Voltando ao cálculo:
Substituindo na primeira equação vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
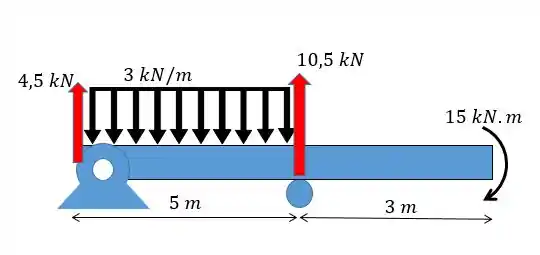
As forças aparecem como:
O momento como:
Mas aqui repare que quando então o carregamento é nulo. Sendo assim não faz muito diferença colocar esse termo. Resumindo, o último termo não precisa ser colocada na equação.
A carga uniforme seria dada por:
Mas perceba que se tivéssemos esse formato estaríamos considerando que essa carga atuaria desde o ponto até e não é isso que acontece!
Existe, portanto, uma falha na aplicação das funções de descontinuidade que se demonstra quando a carga não chega até o final da viga. Mas podemos resolver isso com uma combinação de cargas. Veja o esquema abaixo:
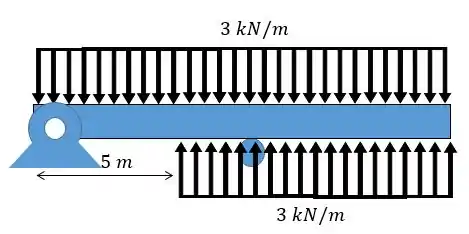
Repara que até temos apenas a carga de e depois temos uma carga de e uma de , assim, elas se anulam e voltamos a ter o carregamento que a questão pede. Portanto, a carga será dada por:
Somando os dois termos (da força e do carregamento uniforme):
Passo 4
Agora que temos o carregamento é só aplicar a equação:
Vamos integrar pela primeira vez:
Agora fazendo a segunda derivada:
A terceira derivada:
A quarta derivada:
Agora temos de achar os valores de e .
Galera, é importante lembrar que essas constantes só aparecem nas duas últimas integrações ok? As duas primeira integrações representam a força cortante e o momento fletor, por isso não é necessário colocar as constantes de integração!
Passo 5
Agora vamos substituir as condições de contorno, como é um pino e uma rótula vamos ter em ambos. Começando pelo pino:
Como no pino e vamos ter:
Agora para a rótula e :
Portanto a nossa equação da linha elástica vale:
E da inclinação:
Como: