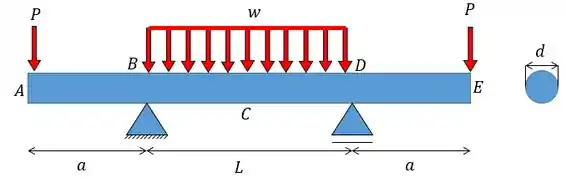
A viga suporta uma carga distribuída e duas cargas concentradas, cada uma com intensidade . Sabendo-se que a viga é feita de uma barra de alumínio de diâmetro e que , e , determinar: a equação que define o carregamento utilizando funções de descontinuidade.
Passo 1
Galera essa questão já começa a misturar os tópicos de função de descontinuidade com linha elástica. Então vamos lembrar que o cálculo da linha elástica é feito como:
Vamos achar a linha elástica utilizando esse tipo de função então e calcular a deflexão e a inclinação. Para isso a gente precisa encontrar primeiro o momento fletor e, portanto, as reações. Vamos fazer isso tudo utilizando o conceito de função de descontinuidade que aprendemos =D
Passo 2
Vamos começar achando as reações nos apoios, para isso a gente vai fazer um desenho das forças:
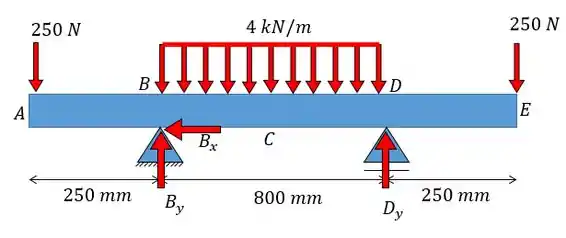
Como não há carga no eixo horizontal então vamos ter que:
Aplicando o somatório dos momentos em vamos ter:
Lembre-se que a força concentrada relativa à carga distribuída atua na metade do carregamento. Aqui vale notar também que vamos utilizar tudo em , beleza?
E aplicando o somatório das forças em vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
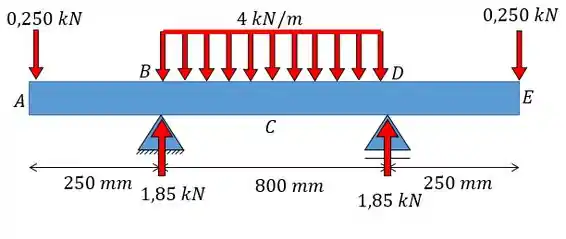
As forças aparecem como:
obs: A força da última extremidade pode ser ignorada, lembra disso!
A carga uniforme deste problema não vai até o final da viga, logo devemos representar como uma combinação de cargas:
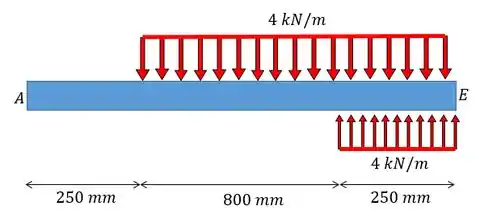
Então vamos ter:
Pessoal, o certo seria somar as forças e carregamentos e obter um grandão, mas como uma equação muito grande fica ruim de ser lida aqui no site então vou deixar esses termos separados mesmo, ok?
Logo, a equção que queremos é:
O motivo dos ficarem separados é unicamente porque não cabem aqui na nossa telinha beleza?