Utilizando as funções de descontinuidade e de singularidade encontre o momento fletor da seguinte viga:
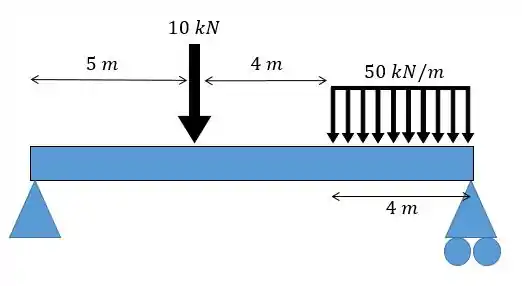
Passo 1
Bom pessoal vamos aplicar o que vimos na teoria e achar o momento fletor utilizando as equações de descontinuidade. A primeira coisa que temos de fazer é achar todas as forças atuantes na barra, então temos de achar as reações nos apoios.
Feito isso vamos colocar tudo em função de cargas e integrar duas vezes para achar o momento fletor.
Passo 2
Vamos achar as reações nos apoios, para isso a gente vai fazer um desenho das forças:
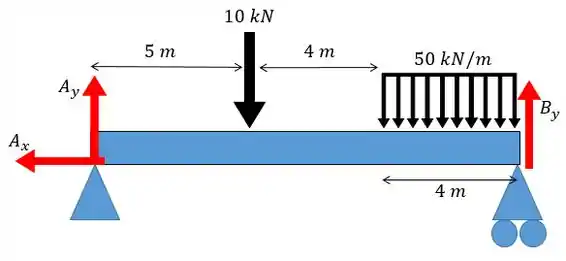
Como há apenas uma força em vamos ter que:
Fazendo o somatório de forças no eixo :
A força exercida pela carregamento uniforme é dada por:
Substituindo na equação:
Agora vamos aplicar o somatório dos momentos em relação ao ponto considerando o sentido anti-horário como positivo:
Lembrando que o ponto de atuação da força exercida pelo carregamento uniforme se encontra na metade do carregamento. Fica assim:
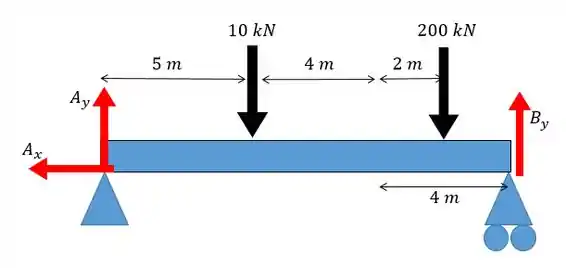
Voltando ao cálculo:
Substituindo na primeira equação vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
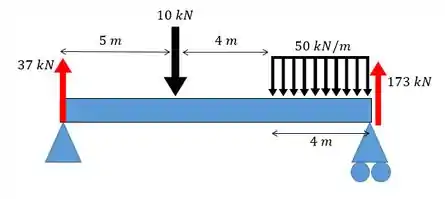
As forças aparecem como:
obs: A força não aparece porque está na extremidade oposta, não precisamos considerar ela.
A carga uniforme é dada por:
Somando os dois termos:
Passo 4
Agora é só integrar uma vez para achar a força cortante.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
E agora para achar o momento fletor é só integrar novamente.
Pronto! temos a nossa resposta do problema!
Ajuda muito não é mesmo? Não precisamos fazer um momento de desenhos e cálculos...
Passo 5
Galera, sei que já temos o resultado final. Mas imagina que o problema pede para calcularmos o momento fletor no ponto .
Nesse caso como e a gente considera esses valores normalmente (e troca por parêntesis só pra frisar que eles vão ser considerados. E elimina o o termo porque . Vamos ficar com: