Encontre a equação da linha elástica para a viga abaixo. Considere constante.
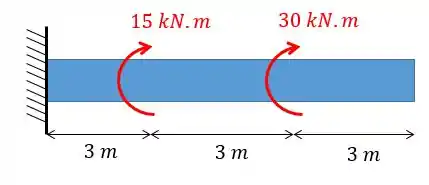
Passo 1
Galera essa questão já começa a misturar os tópicos de função de descontinuidade com linha elástica. Então vamos lembrar que o cálculo da linha elástica é feito como:
Vamos achar a linha elástica utilizando esse tipo de função então e calcular a deflexão e a inclinação. Para isso a gente precisa encontrar primeiro o momento fletor e, portanto, as reações. Vamos fazer isso tudo utilizando o conceito de função de descontinuidade que aprendemos =D
Passo 2
Vamos começar achando as reações nos apoios, para isso a gente vai fazer um desenho das forças:
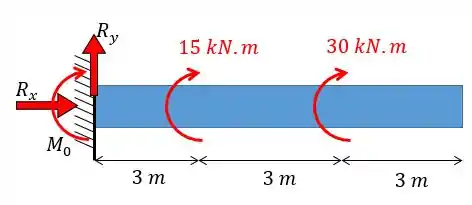
Como há apenas momentos na viga então vamos ter que:
Aplicando o somatório dos momentos vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
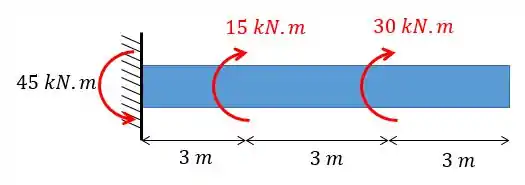
Os momentos aparecem da seguinte forma, lembrando que aqui temos de considerar o sentido anti-horário positivo necessariamente:
Passo 4
Agora é só integrar uma vez para achar a força cortante.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
Vamos lá!
E agora para achar o momento fletor é só integrar novamente.
Pronto! temos a nossa resposta do problema! Perceba que todos os expoentes são iguais a zero, o que significa que nosso momento fletor varia em degrauzinhos. Isso faz total sentido com o nosso carregamento, que é formado por momentos puros.
Passo 5
Mas o problema pede a equação da linha elástica então nós vamos ter que aplicar a seguinte equação:
Substituindo:
Integrando a primeira vez:
Para descobrir o valor de a gente tem que lembrar que , ou seja, essa nossa equação é da inclinação! Como o ponto está engastado então vamos ter , assim:
Repare aqui que muitos dos termos zeraram, não porque , mas sim por causa da própria natureza da função de descontinuidade.
Agora vamos integrar pela segunda vez:
Agora vamos aplicar o mesmo conceito para achar , como em temos um engaste então a deflexão nesse ponto também é zero, logo:
DICA: Para saber quando uma função de descontinuidade deve ser negligenciada, basta lembrar que o termo dentro dos parêntesis bonitinhos nunca pode ser menor do que zero.
Então finalmente vamos ter a equação da linha elástica: