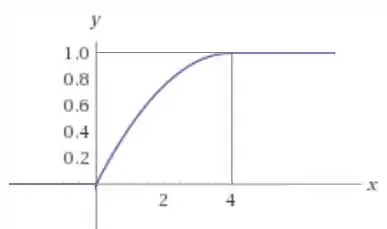
A função de densidade de uma variável aleatória é dada pela função cujo gráfico se encontra na figura:
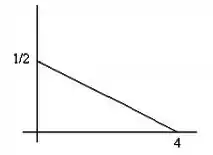
e) Calcule a função de distribuição acumulada e esboce seu gráfico.
Passo 1
Nós sabemos que a FDA é a integral da função de densidade de menos infinito até , certo? Então vamos ter que descobrir primeiro a equação da função de densidade .
Mas olhando o gráfico dela, vemos que é uma reta! E toda reta tem o formato . Para descobrir o valor das constantes e , vamos usar nossos pontos conhecidos no gráfico:
Isso dá pra gente:
Resolvendo esse sisteminha, achamos que e .
Então nossa função de densidade é:
Mas repara que no gráfico essa reta só tá desenhada para os pontos onde , certo? Então esse é o intervalo que nossa função de densidade existe. Para pontos fora desse intervalo, ela vai valer zero.
Passo 2
Agora vamos lembrar a fórmula da FDA:
Onde esse é simplesmente a com reescrito no lugar do , só pra gente não confundir com o do limite de integração. Então:
Uééé, mas por que começou em zero? Porque antes disso nossa função de densidade era zero, ora bolas! Então não vai mudar nada no cálculo começar daí. Integrando temos:
Então a FDA é:
Mas isso aí é só para , certo? Por que é esse intervalo que a função de densidade existe. A expressão completa fica:
Por que na FDA é sempre se estamos antes de existir () e se estamos depois ().
Passo 3
Socorro mas e o gráfico disso? Isso aí é uma equação de 2º grau, gente! Ou seja, é uma parábola! Como a constante que tá multiplicando o é negativa, vai ser uma parábola com a concavidade para baixo.
E a FDA sempre começa com e termina em , certo? Desenhando uma parábola com concavidade para baixo seguindo essas condições, teríamos isso aqui:
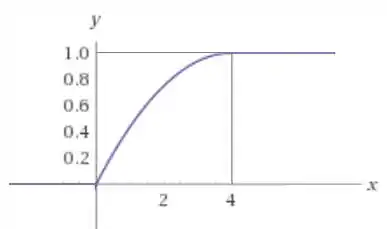
Resposta