AV3 de Cálculo 1 da UFJF - 2019.1

Considere a função definida implicitamente abaixo

O valor do coeficiente angular da reta tangente ao gráfico de no ponto é:

Podemos afirmar:

Considere a função e suas derivadas definidas abaixo

Sobre o crescimento e decrescimento da função podemos afirmar que:

1. é crescente nos intervalos e é decrescente nos intervalos
2. é crescente nos intervalos e é decrescente nos intervalos
3. é decrescente nos intervalos e é crescente nos intervalos
4. é decrescente nos intervalos e é crescente nos intervalos
5. é decrescente nos intervalos e é crescente nos intervalos

Considere a função e suas derivadas definidas abaixo

Sobre os pontos críticos e extremos relativos locais da função , podemos afirmar:

1. o conjunto dos pontos críticos de é , possui máximo relativo em e não possui mínimo relativo
2. o conjunto dos pontos críticos de é , possui mínimo relativo em e não possui máximo relativo
3. o conjunto dos pontos críticos de é . possui máximo relativo em e não possui mínimo relativo
4. o conjunto dos pontos críticos de é . possui mínimo relativo em e não possui máximo relativo
5. não possui pontos críticos nem extremos relativos

Considere a função e suas derivadas definidas abaixo

As assíntotas do gráfico de é correto afirmar que:

1. são as únicas assíntotas verticais e não existem assíntotas horizontais
2. são as únicas assíntotas verticais e é a única assíntota horizontal
3. é a única assíntota vertical e é a única assíntota horizontal
4. é a única assíntota vertical e não existem assíntotas horizontais
5. não existem assíntotas verticais e é a única assíntota horizontal

Usando a regra de L'Hôpital, calcule o limite abaixo

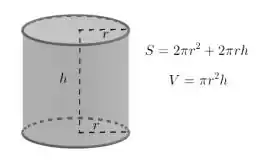
Um cilindro circular reto fechado de altura e raio das bases tem área total igual a e volume . DENTRE TODOS OS CILINDROS DE VOLUME , obtenha as dimensões daquele que tem a menor área total possível.

Uma escada de de comprimento está apoiada em uma parede vertical. A base da escada, que está ́a apoiada no chão, está a sendo empurrada na direção da parede a uma

velocidade constante de . Com que velocidade o topo da escada sobe quando a base da escada está da parede?

Considere a função e suas derivadas definidas abaixo

1. Determine os intervalos onde o gráfico de é côncavo para cima e os intervalos onde o gráfico de é côncavo para baixo.
2. Determine, se existirem, o(s) ponto(s) de inflexão do gráfico de .
3. Esboce o gráfico de