AV3 de Cálculo 1 da UFJF - 2018.2

A sabendo que são números reais não nulos. Sabendo que:

Podemos afirmar:

A derivada da função definida implicitamente abaixo calculada no ponto

Podemos afirmar:

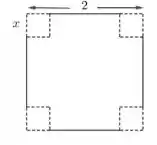
Uma caixa é feita retirando-se quatro quadrados dos cantos de uma folha de papel quadrada de lado e dobrando os lados, como na figura. O tamanho dos lados dos quadrados retirados para que o volume da caixa seja máximo pertence ao intervalo:

O gráfico a seguir representa a derivada de uma função contínua em .

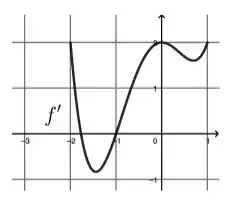
Sobre é INCORRETO afirmar que:

1. é crescente em
2. tem ponto de inflexão em
3. ́e côncava para cima em
4. tem um mínimo local em
5. tem um máximo local em

Considere a função , definida a seguir

É correto afirmar que:

Sobre é CORRETO afirmar que:

1. O valor mínimo de é e o máximo é
2. O valor mínimo de é e o máximo é
3. O valor mínimo de é e o máximo é
4. O valor mínimo de é e o máximo é
5. O valor mínimo de é e o máximo é

O gráfico a seguir representa a função contínua e derivável em .

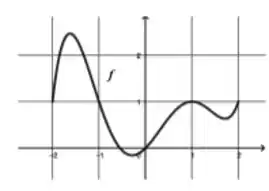
Se no intervalo representado tem pontos críticos e pontos de inflexão, então vale

Considere a funçao definida por:

Sobre as assíntotas do gráfico de f ́é correto afirmar que:

a) são as únicas assíntotas horizontais e é a única assíntotas vertical.

b) é a única assíntota horizontal e é a única assíntotas vertical.

c) é a única assíntota horizontal e não existe assíntotas vertical.

d) são as únicas assíntotas horizontais e não existe assíntota vertical.

e) Não existem assíntotas horizontais e é a única assíntotas vertical.

Uma particula se desloca sobre o gráfico da fun ̧c ̃ao

no quadrante de forma que sua coordenada é o vértice de um triângulo retângulo como na figura abaixo.

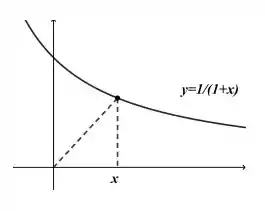
Se a taxa de variação da coordenada é constante igual a , determine a taxa de variação área do triângulo no instante em que .

Uma função tem as seguintes propriedades

1. i) é crescente em _____ e decrescente em ______ .

   ii) ́ é côncava para cima em _____ e côncava para baixo em _____ .

   iii)́ ______ é um ponto de máximo local e ___________ é um ponto de inflexão do gráfico de .

2. Esboce o gráfico de