Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra do Produto e do Quociente

Ver Teoria
Exercício 228123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFJF, Sem Campus, Cálculo 1, AV3 - 2019.1, Questão 6

Considere a função f e suas derivadas definidas abaixo

f ( x ) = - 2 x 2 x 2 - 1

f ' ( x ) = 4 x ( x 2 - 1 ) 2

f ' ' ( x ) = - 4 - 12 x 2 ( x 2 - 1 ) 3

  1. Determine os intervalos onde o gráfico de f é côncavo para cima e os intervalos onde o gráfico de f é côncavo para baixo.
  2. Determine, se existirem, o(s) ponto(s) de inflexão do gráfico de f .
  3. Esboce o gráfico de f

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1.

Essa é uma questão com três letras. Vamos começar pela letra a) Ela pede para determinar os intervalos onde o gráfico de f é côncavo para cima e os intervalos onde o gráfico de f é côncavo para baixo.

Lembram como fazemos isso? Usamos o teste da segunda derivada, isto é, se a segunda derivada for positiva concavidade para cima, e se for negativa concavidade para baixo. A nossa segunda derivada é:

f ' ' ( x ) = - 4 - 12 x 2 ( x 2 - 1 ) 3

Vamos começar calculando suas raízes, temos que

- 4 - 12 x 2 ( x 2 - 1 ) 3 = 0

⇒ - 4 - 12 x 2 = 0

⇒ x 2 = - 1 / 3

Que não tem soluções reais. Logo nosso numerador é sempre negativo, vamos ver o nosso denominador

( x 2 - 1 ) 3

Bem, para - 1 < x < 1 O denominador é negativo, e para valores fora desse intervalo é positivo. Colocando tudo na reta real temos:

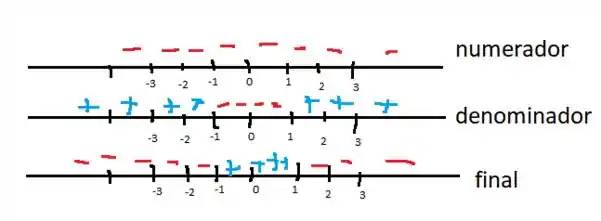
Ou seja, a nossa segunda derivada tem os seguintes sinais

f ' ' ( x ) > 0   s e   - 1 < x < 1

f ' ' ( x ) < 0   c a s o   c o n t r á r i o

Então f é côncava para cima em   - 1 < x < 1 e côncava para baixo caso contrário

Passo 2

Agora, vamos para a letra b ) que pede para determinar, se existirem, o(s) ponto(s) de inflexão do gráfico de f . Bem pontos de inflexão são aqueles onde a derivada segunda é zero, mas vimos no passo anterior que a derivada segunda não tem raízes reais, logo tais pontos não existem!!!

E por fim, temos a letra c ) que pede para esboçarmos o gráfico de f . Mas para isso, precisamos de alguns fatos sobre a f que foram obtidos de outras questões (essa é a última questão de uma série de questões) eles são:

  1. f é decrescente nos intervalos ( - ∞ , - 1 )   e   [ - 1,0 ) e é crescente nos intervalos [ 0,1 )   e   ( 1 , ∞ )
  2. o conjunto dos pontos críticos de f é { 0 } . f possui mínimo relativo em x = 0 e não possui máximo relativo
  3. x = - 1 ,   x = 1 são as únicas assíntotas verticais e y = - 2 é a única assíntota horizontal

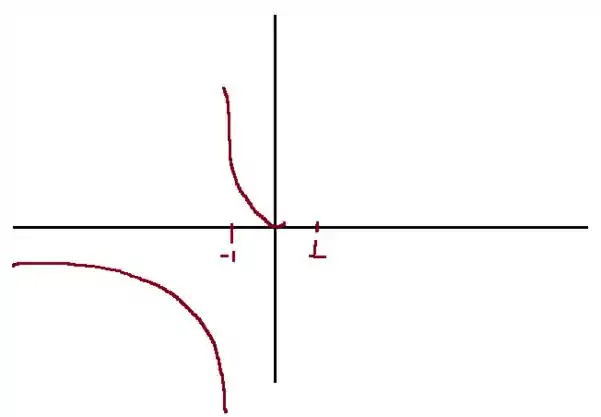
Com essas informações, podemos começar a desenhar o gráfico. usando a primeira informação e o fato que descobrimos que f é côncava para baixo e depois para cima nesse intervalo temos e a terceira afirmação:

Para finalizar, usamos o fato de f ser crescente no intervalo [ 0,1 ) ∪ ( 1 , ∞   ) em conjunto com as concavidades que obtivemos. O que gera

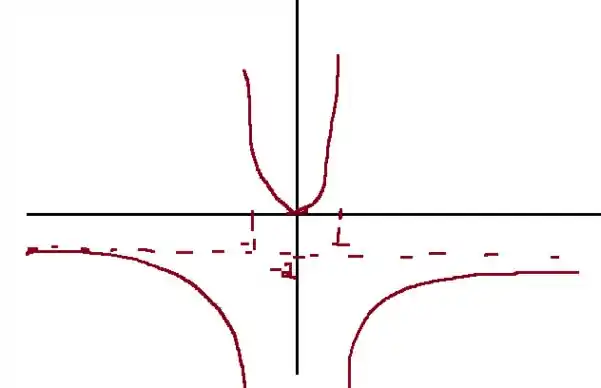
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Se h 2 = 4 e h ' 2 = - 3 , encontre d d x h x x | x = 2
Se f x = e x g x , onde g 0 = 2 e g ' 0 = 5 , encontre f ' 0 .
Se g for uma função derivável, encontre uma expressão para derivada de cada uma das seguintes funções. y = x g ( x ) y = x g x y = g x x
62. a) Se F x = f x g x , onde f e g tên derivadas de todas as ordens, mostre que F ' ' = f ' ' g + 2 f ' g ' + f g ' ' . b) Encontre fórmulas análogas para F ' ' ' e F 4 .c) Conjecture uma fórmula pa
Derive a função: R t = ( t + e t ) ( 3 - t )