Listas de Aplicações de Derivadas de Cálculo 1 da UFSC - Lista 3.9 - Problemas de Otimização
Cálculo 1 - UFSC
Um fabricante de um determinado produto sabe que se produtos forem produzidos, cada um poderá ser vendido por reais. Sabe-se que o custo de produção de produtos é de . Quantos produtos o fabricante deve produzir para obter um lucro máximo e qual será o valor desse lucro?
Ver solução completaAche as dimensões do maior jardim retangular que pode ser fechado com 100 de cerca.
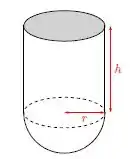
Ver solução completaUm sólido será construído acoplando-se a um cilindro circular reto, de altura e raio , uma semiesfera de raio . Deseja-se que a área da superfície do sólido seja . Determine e para que o volume seja máximo.
Uma caixa com uma base quadrada e sem tampa tem um volume de . Encontre as dimensões da caixa que minimizam a quantidade de material usado.
Ver solução completaUm fabricante de latas cilíndricas de conservas recebe um pedido muito grande de latas com determinado volume . Quais as dimensões que minimizarão a área total da superfície de uma lata como esta, e, portanto, de metal necessário para fabricá-la?
Ver solução completaDuas partículas e movem-se, respectivamente, sobre os eixos e . A função de posição de é e a de , , . Determine o instante em que a distância entre e seja a menor possível.
Ver solução completaAchar dois números positivos cuja soma seja e cujo produto seja o maior possível.
Ver solução completaAo preço de R$ 1,50, um vendedor pode vender 500 unidades de uma certa mercadoria que custa R$ 0,70 cada. Para cada centavo que o vendedor abaixa no preço, a quantidade vendida aumenta em 25 unidades. Que preço de venda maximizaria o lucro?
Ver solução completaDuas partículas e movem-se, respectivamente, sobre os eixos e . A função de posição de é e a de , , . Determine o instante em que a distância entre e seja a menor possível.
Ver solução completaDois produtos e , são produzidos por determinada fábrica. Se for o custo total de produção numa jornada de 8 horas por dia, então , onde e são o número de máquinas que são usadas para produzir e , respectivamente. Se durante a jornada de horas tivermos máquinas em funcionamento, determine quantas devem produzir e quantas devem produzir , para que o custo total seja mínimo.
Ver solução completa