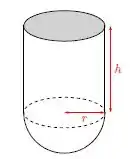
Um sólido será construído acoplando-se a um cilindro circular reto, de altura e raio , uma semiesfera de raio . Deseja-se que a área da superfície do sólido seja . Determine e para que o volume seja máximo.
Passo 1
Pessoal, a área da superfície do sólido será a soma da área lateral do cilindro , da área do fundo do cilindro e da metade da área de uma esfera :
Assim, acabamos de achar a altura do cilindro em função do raio .
Passo 2
Queremos maximizar o volume , dado pela soma do volume do cilindro e da metade do volume de uma esfera :
Vamos substituir a expressão de ?
Passo 3
Agora, vamos derivar a função e igualar a zero:
Conforme já vimos, o valor de correspondente pode ser calculado assim: