Lista de Aplicações Cálculo 1 - UnB de Cálculo 1 da UnB - Lista 4

Duas partíıculas carregadas com cargas de módulos interagem com uma força

eletrostática. Segundo a Lei de Coulomb, o módulo dessa força, em Newtons, é modelado

pela função

dada por

, onde e resolva os itens a seguir.

(a) Encontre (dez milhões de Newtons).

(b) Encontre (um milionésimo de Newton).

(c) Determine .

(d) Faça um esboço do gráfico de .

A figura abaixo ilustra um corpo de massa pendurado no teto de um trem bala por

um fio inextensível de comprimento . Quando o trem possui aceleração, o pêndulo

se encontra inclinado, fazendo um ângulo com a vertical. Pode-se provar que, se é

a aceleração da gravidade local, então . Como temos que , onde a função é a função inversa da

tangente. Supondo que , resolva os itens seguintes.

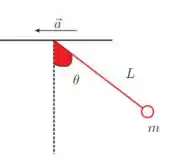
(a) Sabendo que , encontre

e

(b) Se a aceleração do trem tomar valores cada vez maiores, o ângulo se aproxima de que valor? E se , então tende para algum número?

(c) Faça um esboço dos gráficos de , com suas

assíntotas.

Considerando a função

definida para , resolva os itens abaixo.

(a) Calcule os limites no infinito da função e, em seguida, determine a(s) assíntota(s)

horizontal(is) do gráfico da função , se esta(s) existir(em).

(b) Calcule os limites laterais de no ponto e, em seguida, determine a(s)

assíntota(s) vertical(is) do gráfico da função , se esta(s) existir(em).

(c) Faça um esboço do gráfico de .

Para cada , o número positivo pode ser caracterizado como área da região

limitada pelo eixo , pelas retas verticais e pelo gráfico da função

. Por exemplo, o número é a área da região compreendida entre o gráfico

da função e as retas . Na figura foram destacados ainda três

retângulos de base unitária cujas alturas são.

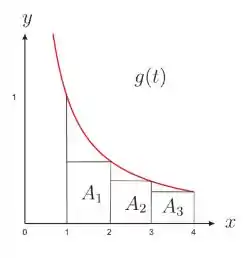
(a) Determine as areas dos retângulos indicados,

e faça sua soma.

(b) Usando o resultado anterior, justifique a desigualdade

.

(c) Dada uma constante arbitrariamente grande,

mostre que se ,então .

Conclua daí que: .

(d) Sabendo que para todo tem-se

investigue a existência de .

(e) Lembre que e calcule . Esboce o gráfico das funções