Para cada , o número positivo pode ser caracterizado como área da região
limitada pelo eixo , pelas retas verticais e pelo gráfico da função
. Por exemplo, o número é a área da região compreendida entre o gráfico
da função e as retas . Na figura foram destacados ainda três
retângulos de base unitária cujas alturas são.
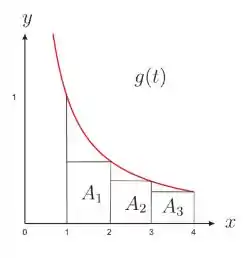
(a) Determine as areas dos retângulos indicados,
e faça sua soma.
(b) Usando o resultado anterior, justifique a desigualdade
.
(c) Dada uma constante arbitrariamente grande,
mostre que se ,então .
Conclua daí que: .
(d) Sabendo que para todo tem-se
investigue a existência de .
(e) Lembre que e calcule . Esboce o gráfico das funções
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1. Essa questão é muito bacana, ela é um roteiro que introduz a noção de integral, e o jeito de utilizarmos funções contínuas para obtermos relações de funções discretas.
Bem, então vamo começar pela letra a)
Passo 2
Nosso objetivo na letra a) é calcular a área dos retângulos . Suas áreas serão sua base vezes a altura, logo:
Então a soma será:
Passo 3
Agora vamos fazer a letra b). Queremos mostrar que . Usando o fato descrito no enunciado que diz que pode ser caracterizado como área da região
limitada pelo eixo , pelas retas verticais e pelo gráfico da função
. Temos que será uma aproximação da área limitada pelo eixo , pelas retas verticais e pelo gráfico da função , e será menor. Então,
Então
Bacana, né?

Passo 4
Podemos fazer a letra c) agora. Ela pede para mostrar que: Dada uma constante arbitrariamente grande, mostre que se ,então .
Mas como vamos fazer isso? Podemos usar o resultado da questão anterior!!!! temos que se
(aplicando o log)
(a desigualdade se mantém pois como o log é definido como a soma de áreas positivas ele será uma função crescente)
(usando o resultado do passo anterior)
Mas se isso ocorrer, então sempre podemos escolher um tal que se então
Isso quer dizer que é ilimitada. Ou seja
Passo 5
No passo anterior, mostramos que é uma função ilimitada. Agora vamos usar esse resultado para fazer a letra d).
Essa letra pede para investigar a existência de .Sabendo que para todo tem-se .
Bem, no passo anterior, mostramos que
Ora, mas se então
tranquilinho, né?

Passo 6
Para finalizarmos essa questão, só nos resta fazer a letra e). Ela pede o seguinte:
calcule . E esboce o gráfico das funções
Vamos começar calculando .
mas vimos no passo anterior que converge para o infinito quando for grande. Então será alguma coisa pequena dividida por algo que cresce ilimitadamente (muito grande). Logo será bem próximo de zero. isto é:
Agora podemos esboçar os gráficos das funções:
Temos que é uma função sempre positiva, crescente (e muito) e ilimitada. então seu gráfico será:
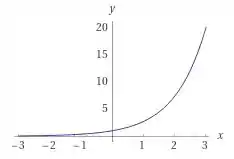
Para o gráfico de podemos usar o gráfico de e espalhá lo em relação ao eixo , pois
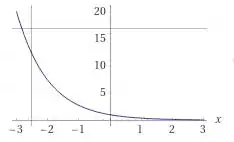
e por último o gráfico de . Sabemos que o gráfico será crescente, e sempre menor que , mas não cresce na mesma intensidade que .
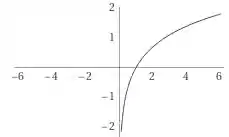

Prontinho pessoal. Com isso terminamos mais uma questão de Calculo 1, espero que os passos tenham ficado claros. Até a próxima!!!
Resposta
Ei, a resposta está no passo a passo :)