Considerando a função
definida para , resolva os itens abaixo.
(a) Calcule os limites no infinito da função e, em seguida, determine a(s) assíntota(s)
horizontal(is) do gráfico da função , se esta(s) existir(em).
(b) Calcule os limites laterais de no ponto e, em seguida, determine a(s)
assíntota(s) vertical(is) do gráfico da função , se esta(s) existir(em).
(c) Faça um esboço do gráfico de .
Passo 1
Fala pessoal, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1. Essa é bem bacana, pois iremos trabalhar nossas habilidades de desenhar um gráfico.
Mão na massa!!!
Passo 2
Vamos começar fazendo a letra a). Para essa letra, nosso objetivo é obter os limites de no infinito e suas assíntotas verticais.
Vamos começar calculando os limites nos infinitos, isto é, queremos saber quem são
e
Como vamos fazer isso? o que vocês acham?

vamos tentar reescrever nossa de uma forma esperta
(colocando x em evidência)
(tirando da raiz)
agora podemos aplicar os limites
(pois 1/x é decrescente)
e temos que
(pois 1/x é decrescente)
Então nossos limites no infinito são iguais a 1 e -1.
Logo, nossas assíntotas horizontais são as retas,
Passo 3
Vamos fazer a letra b). Precisamos calcular as assíntotas verticais. Como as calculamos?Vocês lembram?

As assíntotas verticais são as retas da forma com constante tal que o valor da função naquele ponto explode, isto é, é mais ou menos infinito, ou “os dois”. Que ocorre quando temos uma “divisão por zero”
No caso da nossa função o valor de para o qual ele “explode” ocorre quando , pois para esse valor o denominador da função é ZERO
Então vamos calcular os limites laterais entorno do ponto , esses limites são definidos como:
e
Vamos começar pelo primeiro limite:
Bem, como no ponto Já sabemos que a função vai “explodir”, a única coisa que precisamos obter é a direção, isto é, se vai para mais infinito ou menos infinito.
então, para o sinal da nossa fica:
então
para
então
de forma análoga obtemos obtemos que para o sinal da nossa fica:
para
então
prontinho para finalizar a questão só precisamos desenhar o gráfico de

Passo 4
Na última letra, precisamos esboçar o gráfico de , mas essa tarefa é bem mais fácil, pois já calculamos as assíntotas verticais e horizontais de . Então só falta verificamos se tem alguma raiz real.
Logo não tem raízes reais, o que implica que seu gráfico não corta o eixo . Então o gráfico de fica da seguinte forma:
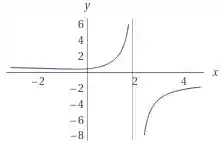

Prontinho pessoal. Com isso terminamos mais uma questão de Calculo 1, espero que os passos tenham ficado claros. Até a próxima!!!
Resposta
Ei, a resposta está no passo a passo :)