1º EE de Calculo 2 da UFPE - 2017.1

Considere o elipsoide

1. Numa vizinhança de , suponha que conseguimos descrever o elipsoide como o gráfico de uma função diferenciável, isto é, escrever .

Determine e para .

2. Nas mesmas condições do item anterior, considere e . Determine e para .

Considere a função

1. Determine o domínio de
2. Suponha que queiramos estender para todo o , ou seja, encontrar uma função que seja igual a dentro de (letra mas que fosse definida em todo o . Seria possível encontrar uma tal que fosse contínua? Justifique.
3. Seria possível encontrar uma que fosse diferenciável? Justifique.
4. Seria possível encontrar uma tal que admitisse funções derivadas parciais e contínuas? Justifique

A tabela abaixo representa os valores, em alguns pontos, da função que admite derivadas parciais segundas contínuas:

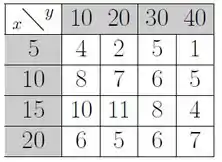
1. Estime os valores de e
2. Estime o valor de . Dica: olhe para uma tabela de estimativas de .

Observação: tais estimativas devem ser coerentes com o que vimos em sala e não meras adivinhações.

Considere

1. Determine a equação do plano tangente ao gráfico de em ; e também a diferencial
2. Numa vizinhança de , calcule e considerando as variações e
3. O que significa a diferença entre os valores que você encontrou no item anterior em termos práticos? Justifique.