A tabela abaixo representa os valores, em alguns pontos, da função que admite derivadas parciais segundas contínuas:
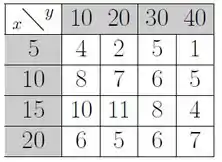
- Estime os valores de e
- Estime o valor de . Dica: olhe para uma tabela de estimativas de .
Observação: tais estimativas devem ser coerentes com o que vimos em sala e não meras adivinhações.
Passo 1
Então, a gente tá tendo que calcular a derivada parcial em relação a , sendo que não temos a definição de e a única informação que temos são os valores de em alguns pontos. Como fazer?
Bom, já sei que não dá pra calcular a derivada normalmente, como estamos acostumados, pois não temos a definição da função.
Vamos apelar pra a tal da definição então, né mores?
Você lembra como era?
Ok, mas de novo caímos no problema de não tem a expressão de .
Mas aí eu te pergunto: não ter a expressão de significa não poder calcular o valor exato da derivada. Mas isso não nos impede de estimar, que é, afinal, exatamente o que a questão tá pedindo. Acabou que não te perguntei nada, né? Rs
Então, podemos tirar esse limite e aproximar as paradas.
Passo 2
Nossas estimativas vão ficar então
Onde tínhamos , a gente estipulou um valor pro (e colocou o de interesse mesmo), de modo a termos uma aproximação.
Agora, olhando na tabela e substituindo os valores, ficamos com
Passo 3
Agora queremos a derivada segunda de em relação a .
De novo, não temos a expressão de , então vamos apelar para a definição de derivada parcial de ordem superior e dar aquela aproximada marota.
A definição é
Tirando o limite e aproximando, utilizando nossos valores:
Ora, veja que surpresa: teremos que usar as derivadas parciais que calculamos na letra .
Assim