P1 de Física 1 - FIS1033 da PUCRIO - 2017.2

Parte I:

Duas pedras são largadas da beira de um precipício de 60,0 𝑚, sendo a segunda pedra 1,60 𝑠 após a primeira. Encontre a posição, abaixo do topo do precipício, em que está a segunda pedra quando a separação entre as duas é de 36,0 𝑚.

Adote:

Parte III:

Uma força atua sobre o bloco conforme a figura ao lado, produzindo o movimento dos blocos , e juntos sobre uma superfície áspera com coeficiente de atrito cinético . As massas desses blocos são respectivamente, e .

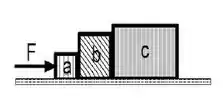
(e) Determine a força que o bloco faz sobre o .

1-( )

2-( )

3-( )

4-( )

5-( )

Parte II:

Coloque V de verdadeiro na resposta correta. Justifique sua opção usando leis físicas.

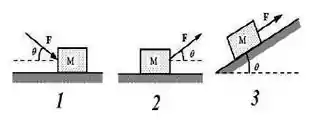
(d) Observe as situações da figura. A força normal sobre o bloco M tem módulo igual a nas seguintes situações:

1-( ) somente em 1.

2-( ) somente em 2.

3-( ) em 1 e 2.

4-( ) em 2 e 3.

5-( ) em 1, 2, 3.

Parte II:

A inclinação de em uma curva com raio na pista de corrida de carros permite que atinjam a velocidade máxima de sem derrapar para fora da pista. Admita o valor de para a massa de um desses carros. Suponha o carro como uma partícula.

(c) Determine o coeficiente de atrito estático dos pneus com a pista.

Parte I:

Uma caixa de massa está sobre um plano inclinado que faz um ângulo com a horizontal. Ela está ligada por uma corda de massa desprezível, que passa por uma roldana ideal, a uma outra caixa de massa , conforme a figura ao lado. Os planos inclinados fazem entre si e não possuem atrito.

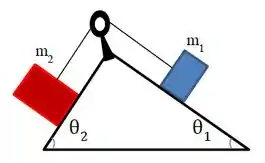
(a ) Faça os diagramas de forças dos blocos 1 e 2.

(b) Determine o módulo da aceleração de cada bloco.

(c) Encontre o módulo da tensão 𝑇 na corda.

Parte I:

Um corpo de massa suspenso por um fio de comprimento , que faz um ângulo com a vertical, gira descrevendo uma circunferência de raio . Esse dispositivo é designado pela expressão pêndulo cônico.

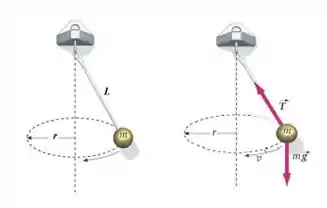
(a) Obtenha uma expressão literal para o período desse pêndulo em função de , e . A expressão pode conter , desde que seja indicada outra fórmula para calculá-lo em termos das grandezas pedidas.

(b) Considere , e . Calcule o período desse pêndulo.

Parte II:

Uma partícula P se move com velocidade escalar constante sobre uma circunferência de raio (figura abaixo) e completa uma volta a cada . A partícula passa pelo ponto no instante . Nesse mesmo instante um atleta A passa pelo mesmo ponto com velocidade constante, correndo ao longo do eixo . O ponto designa a origem de um referencial () em repouso em relação ao solo. Expresse os resultados em função dos vetores unitários.

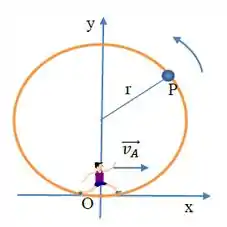
(a ) Encontre a posição da partícula em relação a , nos instantes e .

(b ) Obtenha o deslocamento da partícula entre 𝑒 .

(c ) Calcule a velocidade da partícula no instante .

(d ) Determine a velocidade da partícula em relação ao atleta no instante . Admita que o atleta A possui a mesma velocidade da partícula P na origem do referencial .