P2 de Física 1 - FIS1033 da PUCRIO - 2020.1

. Um avião aeromodelo (massa ) voa em um círculo horizontal de raio com velocidade escalar constante , preso a um fio ideal que exerce a força de tração , fazendo um ângulo de com a horizontal que passa pelo centro do avião. A força de sustentação aerodinâmica faz um ângulo de com a vertical que passa no centro do avião. A figura abaixo mostra as forças que atuam sobre o avião. Determine e a tração do fio .

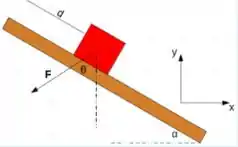
. Um bloco de massa é deslocado para cima, por uma força constante, uma distância ao longo de um plano inclinado. O plano está inclinado de em relação à horizontal, e a força faz um ângulo com a vertical. Determine o trabalho realizado pela força ao longo do deslocamento. Utilize o sistema de coordenadas indicado na figura.

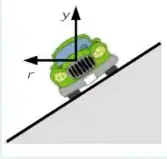
. Um automóvel descreve uma curva com inclinação como indicado na figura. O coeficiente de atrito estático é e o raio da trajetória circular é . Nestas condições o automóvel pode se manter na curva sempre que sua velocidade escalar esteja dentro de certos valores máximos e mínimos. Determine a velocidade mínima com a qual o carro pode fazer a curva sem deslizar.

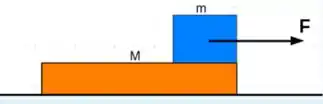
. A figura ilustra um bloco de massa sobre uma prancha de massa apoiada sobre um piso horizontal perfeitamente liso. Considere o coeficiente de atrito estático entre o bloco e a prancha. Determine o maior valor possível do módulo de que permita movimento solidário dos dois corpos (sem deslizamento relativo) e indique quais são pares ação reação entre o bloco e a prancha.

. Um corpo desliza em um piso horizontal no sentido positivo do eixo enquanto uma força age sobre ele. O corpo parte do repouso na posição e se move até ficar momentaneamente em repouso. Determine o valor máximo da energia cinética adquirida pelo corpo e em que posição ela ocorre, determine também, depois de iniciado o movimento em que posição o corpo fica em repouso momentaneamente.

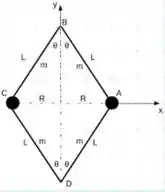
. O sistema mostrado na Figura é formado por quatro barras iguais de massa e comprimento e por duas massas pontuais iguais de massa presas às barras nos pontos e . Sabe-se que o momento de inércia de uma barra que forma um o ângulo com o eixo de rotação que passa pelo seu centro de massa é , . Determine o momento de inércia do sistema em torno do eixo .

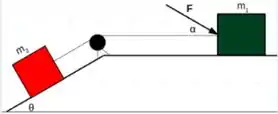
. Na figura, o bloco tem peso e bloco tem peso e está sobre uma rampa que faz com a horizontal. Uma força com módulo é aplicada sobre o bloco fazendo um ângulo de com a horizontal. Considere que não existe atrito entre os blocos e as superfícies e que a corda e a polia são ideias. Determine a aceleração dos blocos e determine se o bloco está subindo ou descendo a rampa. Considere .

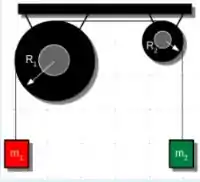
. Os cilindros mostrados na Figura têm raios e , massas e e momentos de inércia em relação a seus centros de massa determinados pela relação geral . Os cilindros são livres para girar em torno de eixos horizontais fixos, perpendiculares à figura e que passam pelos respectivos centros de massa. O fio de massa desprezível passa sem deslizamento pelos cilindros e suas pontas livres estão presas a corpos de massas e , em repouso na mesma altura. Determine a aceleração dos corpos e a velocidade do corpo quando este se deslocou . Adote .

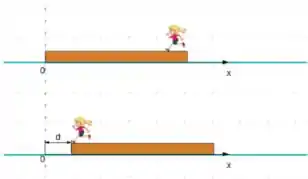
. Uma moça está parada no extremo direito de uma plataforma plana, que, por sua vez, também se encontra em repouso com relação à superfície de gelo em que se apoia. A moça, então, começa a correr para a esquerda com velocidade constante em relação à plataforma. Não há atrito entre a plataforma e a superfície de gelo, a massa da moça é , a massa da plataforma é e o tamanho da plataforma é . Tome a posição inicial do extremo esquerdo da plataforma em como mostrado na figura. Encontre o centro de massa do sistema (moça-plataforma) antes da moça começar a se mover. Quando a moça chega no extremo esquerdo da plataforma, esta se moveu uma distância (como na figura) determine .

. O sistema de transporte de passageiros sobre trilhos entre a base e o topo de uma montanha, mostrado na figura, é composto de um vagão (massa ), uma mola que obedece a lei de Hooke , polia e cabo ideais, e um contrapeso (massa ). O coeficiente de atrito cinético entre o vagão e os trilhos na montanha é . O ângulo entre a montanha e a horizontal é . O vagão, travado na base da montanha, recebe passageiros de massa . Em seguida, a trava é retirada, o vagão sobe a montanha e, ao atingir o topo, comprime a mola até parar. A distância total percorrida desde a retirada da trava até a compressão total da mola é de . Determine qual é a velocidade do vagão após percorrer os primeiros e a distância percorrida pelo vagão desde o instante em que toca a mola até parar.

. Um bloco de massa é solto do repouso de uma altura (posição ) na pista ilustrada na figura. A pista é sem atrito, a menos de um trecho de comprimento e coeficiente de atrito cinético . O bloco chega à mola de constante elástica e a comprime até chegar a um repouso momentâneo. Determine a compressão máxima da mola, a velocidade do bloco em , quando este passa pelo trajeto pela segunda vez, a posição que o bloco para finalmente. Adote