Parte I:
Duas pedras são largadas da beira de um precipício de 60,0 𝑚, sendo a segunda pedra 1,60 𝑠 após a primeira. Encontre a posição, abaixo do topo do precipício, em que está a segunda pedra quando a separação entre as duas é de 36,0 𝑚.
Adote:
Passo 1
Temos que a pedra 1 foi largada primeiro e ganha velocidade em direção ao chão realizando um movimento uniformemente variado (MUV). Logo depois ( depois, para ser mais exato) a segunda pedra é largada.
Para visualizar melhor a situação, dá uma olhada nesse desenho aqui:
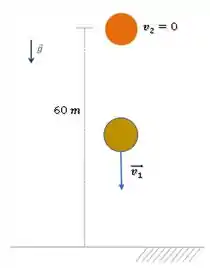
Um erro comum é achar que a distância entre as pedras, quando a segunda é largada, vai se manter durante o trajeto pois elas estão sob a mesma aceleração. Porém, isso está errado, a pedra 1 ao longo de todo o trajeto vai ter uma velocidade maior que a pedra 2 e, por isso, vai se afastar cada vez mais dela até atingir o chão.
As pedras vão se afastando ao longo da queda, em algum momento elas estarão à de distância uma da outra. A questão pede qual a posição da segunda pedra nesse instante.
Passo 2
Vamos escrever a equação da posição de cada pedra em função do tempo. Em um MUV, podemos escrever a equação da posição em função do tempo com:
Onde é a posição no instante , é a posição inicial, é a velocidade inicial, é a aceleração e é o tempo.
Vamos considerar que a pedra 1 tem uma posição inicial de , velocidade inicial nula (largada) e a aceleração vai ser a da gravidade:
A pedra 2 vai ter os mesmos parâmetros que a pedra 1, com exceção do instante inicial. Se ela foi largada após a pedra 1, podemos ajustar a equação da seguinte maneira:
Dessa forma, quando , vamos ter , ou seja, o momento inicial do lançamento da pedra 2.
A distância entre as pedras vai ser a diferença das posições () de cada uma:
Colocamos menos apenas porque a segunda pedra estará sempre acima da primeira, então será positivo. Mas, sabendo interpretar, pode-se usar outra convenção.
Passo 3
Agora que já temos a expressão da distância, vamos substituir a distância de para achar o instante em que isso ocorre:
Substituindo :
Então, sabemos que em , as pedras estão afastadas em .
Passo 4
Já sabemos o instante em que isso ocorre, só falta achar a posição da pedra 2 nesse instante:
A questão pede a posição abaixo do topo da superfície, então se a altura total é e a pedra está a uma altura de , ela desceu: