P3 de Física 1 - FIS1033 da PUCRIO - 2017.2

Considere agora um disco horizontal de raio com quatro hastes conforme a figura ao lado. NÃO é o carrossel do item anterior. Duas pessoas empurram esse disco no sentido anti-horário. Veja a figura abaixo com vista de cima. A força de cada pessoa tem módulo constante , sendo tangente à borda. Não há atrito entre o eixo central e o disco. O sistema disco-hastes tem momento de inércia .

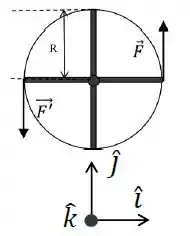
(b) Calcule a aceleração angular do sistema disco-hastes.

Considere o carrossel, da figura abaixo, como um disco de massa e raio . As barras horizontais são finas, têm massa e comprimento . As barras verticais também são finas, possuem massa e altura . O eixo central é constituido por um cilindro de massa e raio desprezíveis.

Dados:

Disco: ;

Haste: ;

;

(a) Calcule o momento de inércia desse carrossel em relação ao eixo central vertical (CM).

A figura mostra uma barra homogênea vertical de comprimento e massa , em repouso, apoiada em um plano horizontal sem atrito, que pode girar em torno de um eixo em sua extremidade. Veja a figura. Uma partícula de massa e velocidade perpendicular à barra se desloca sobre o plano. Ela colide com a barra em um ponto distante do eixo, ficando grudada na barra.

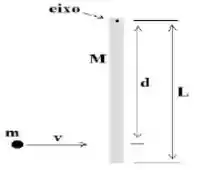
Dado: Haste:

(a) Considere a colisão. Marque com as grandezas físicas conservadas e com as não conservadas. Justifique TODAS as suas escolhas.

1-( ) Momento linear da partícula, pois...

2-( ) Momento linear do sistema barra-partícula, pois...

3-( ) Energia cinética do sistema barra-partícula, pois...

4-( ) Momento angular do sistema barra-partícula em relação ao eixo, pois...

(b) Obtenha uma expressão literal para o valor da velocidade angular do sistema barra-partícula imediatamente após o impacto em função dos dados fornecidos. Justifique claramente a lei física utilizada.

Um atleta ao fazer exercício de flexão no solo para em equilíbrio estático na posição superior, desenhada abaixo. Seu corpo guarda um ângulo com a horizontal. Considere o corpo como uma barra fina, homogênea de massa , apoiada em um ponto O localizado no ponto de contato da extremidade dos pés com o solo. Admita o centro de massa (CM) distante do eixo de rotação. Considere os braços na vertical, de massa desprezível, fazendo uma força total vertical sobre um ponto B nos ombros. O ponto B dista do eixo de rotação O. A aceleração da gravidade é .

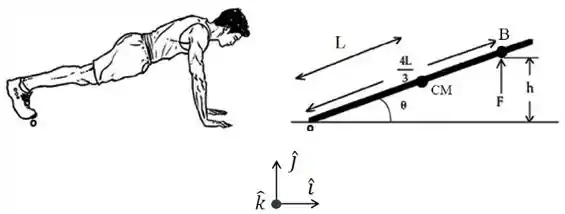
(a) Encontre uma expressão literal para o valor da força aplicada em B em função dos dados fornecidos.

(b) Obtenha uma expressão literal para o módulo da força normal que o solo produz sobre os pés do atleta em função dos dados fornecidos.

Uma esfera maciça em repouso está sobre um plano inclinado e possui uma fita ideal enrolada em torno de sua periferia vertical. Essa fita passa em polia ideal e está ligada a um bloco. Veja figura. Após liberar o conjunto, a esfera sobe o plano sem deslizar e o bloco desce.

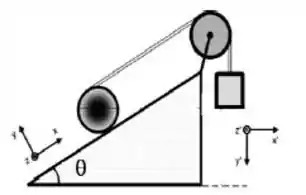
Encontre uma expressão literal para o módulo da aceleração do CM da esfera e da aceleração do bloco. São dados o raio da esfera 𝑅, o ângulo 𝜃, as massas da esfera 𝑀 e do bloco 𝑚 e a aceleração da gravidade 𝑔. A aceleração da fita no ponto superior da esfera é duas vezes a aceleração do CM da esfera.

Dados: Esfera:

(a) Escreva a equação do movimento para o bloco acompanhada do respectivo diagrama de corpo livre.

(b) Escreva a equação do movimento de translação da esfera acompanhada do respectivo diagrama de corpo livre. Faça o mesmo para a equação do movimento de rotação da esfera. Escreva também a condição de rolamento sem deslizamento.

(c) Resolva o sistema de equações e encontre uma expressão literal para o módulo da aceleração do CM da esfera em função dos dados fornecidos.