P3 de Física 1 - FIS1033 da PUCRIO - 2019.1

Uma partícula pontual de massa m = 1,0kg se move sobre uma superfície sem atrito com velocidade constante v = 3,0m/s. Nessa mesma superfície existe um disco homogêneo de raio R =0,50 m e massa M =10 kg que gira com velocidade angular desconhecida (inclusive seu sentido) ao redor de um eixo fixo preso a seu centro de massa. Ao alcançar o disco, a partícula se agarra a ele formando um sistema composto.

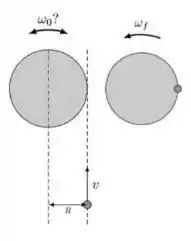
1. Se a velocidade angular final do sistema, com relação ao centro de massa do disco é = 2,0rad/s no sentido anti-horário, calcule a velocidade angular Inicial do disco e indique seu sentido (horário ou anti-horário).

Um disco isolado de forças externas possui raio R e massa m e é feito de um material capaz de se reorganizar internamente. Inicialmente o material está homogeneamente espalhado por todo o disco e possui velocidade angular em torno do centro de massa. Num outro instante, toda a massa se aglomera na borda.

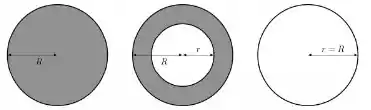
b) Encontre a velocidade angular final em função da velocidade angular inicial, justificando seu raciocínio com base em princípios físicos.

Uma bola de basquete (massa M = 600g e raio R= 12,0cm) sobe um plano inclinado (θ = 30) rolando sem deslizar. Na base do plano, o topo da esfera tem velocidade v = 5,00m/s.

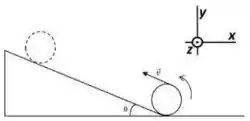
c) Calcule o trabalho total sobre a bola necessário para fazê-la parar.

d) Calcule a distância D que a bola percorre ao longo do plano inclinado até parar.

Uma bola de basquete (massa M = 600g e raio R= 12,0cm) sobe um plano inclinado (θ = 30) rolando sem deslizar. Na base do plano, o topo da esfera tem velocidade v = 5,00m/s.

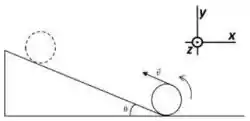
1. Faça um diagrama de corpo livre que represente a bola num ponto qualquer do plano inclinado.
2. Calcule o módulo do torque resultante () sobre a bola e forneça sua direção e sentido em termos dos vetores unitários de acordo com o sistema de coordenadas da figura.

Uma haste homogênea de comprimento L e massa M está presa por uma das extremidades a uma parede pelo ponto O. A haste é mantida na horizontal por uma corda que se prende a uma distância igual a 5L/6 e faz um angulo θ = 36,8° com a haste. Sobre a haste existe ainda uma massa pontual m posicionada à distância x do centro de massa da haste. A força da parede sobre a haste está representada na figura como

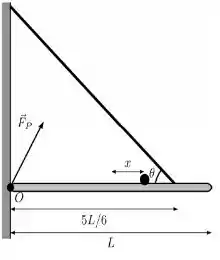
1. Calcule a expressão literal para o momento de inércia I do sistema [haste + massa pontual] com relação a um eixo perpendicular à figura que atravessa o ponto O.

Nos próximos itens, adote: M = 100 kg, m = 12,0 kg e L = 1,20 m.

2. Sabendo que a tensão T na corda não pode exceder 1160 N, encontre o valor máximo de x para que a corda não se rompa.
3. Na situação do item (b), encontre o módulo da força que a parede realiza na haste.
4. Suponha que a massa m se encontra a um valor x = 0,25m e que a corda se rompeu. No instante que a corda se rompe, calcule a aceleração angular α do sistema.