P2 de Física 1 - FIS1033 da PUCRIO - 2018.1

Uma partícula (1) de massa se move na direção positiva do eixo com velocidade no topo de uma mesa sem atrito de altura . Ao final da mesa encontra-se uma partícula (2) de massa . Ignore a dimensão das partículas.

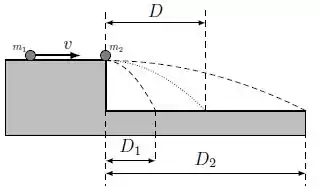
b) Supondo que a colisão entre as partículas foi perfeitamente inelástica, encontre a nova distância percorrida pelas partículas grudadas, em relação a base da mesa (na figura a distância é representada por , a trajetória é descrita pela linha pontilhada). O tempo de queda também é .

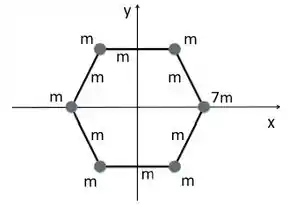
Um sistema hexagonal é formado por hastes idênticas, de massa , e tem por vértices cinco partículas de massa e uma partícula de massa . Encontre a posição (,) do CM desse sistema, sabendo que cada lado do hexágono uniforme vale e que seu centro se encontra em (,). Justifique sua resposta.

Entre e , um corpo (1) de massa se move na direção horizontal positiva (), com velocidade . Ele então colide, em , com um corpo em repouso (2), de massa , e os dois corpos saem grudados.

a) Calcule a velocidade dos corpos 1 e 2 após a colisão.

Em , o corpo 2 explode enviando um fragmento de massa com uma velocidade na direção positiva do eixo .

b) Calcule a velocidade do resto do sistema após .

c) Calcule a velocidade do CM total (corpos 1 e 2, inteiros ou não) para , e .

Um bloco de massa encontra-se a uma altura a partir do topo de uma mola relaxada de constante elástica . Use para a aceleração da gravidade. Após o bloco ser solto e tocar a mola, determine em termos de , e :

a) Qual a compressão da mola onde o bloco tem aceleração nula?

b) Determine a máxima compressão da mola.

Uma partícula (1) de massa se move na direção positiva do eixo com velocidade no topo de uma mesa sem atrito de altura . Ao final da mesa encontra-se uma partícula (2) de massa . Ignore a dimensão das partículas.

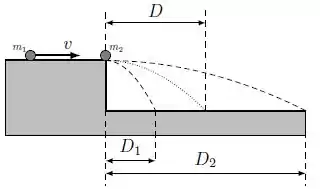
a) Supondo que a partícula (1) colide com a partícula (2) elasticamente como é descrito na figura, encontre a distância total percorrida por cada partícula em relação a base da mesa (na figura as distâncias são representadas por e , suas trajetórias são descritas pelas linhas tracejadas). O tempo de queda é .

Na figura abaixo estão indicadas 3 posições identificadas pelas letras , e . Um Bloco de massa inicialmente em repouso a uma altura a partir do solo está em contato com uma mola comprimida. A mola possui constante elástica .

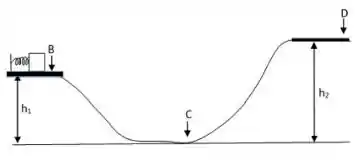
Após a mola ser solta e o bloco se desprender, o bloco desliza sem atrito passando pelo ponto que se encontra na mesma altura . Segue descendo por uma rampa até o ponto . Neste ponto o bloco possui velocidade . Após passar o ponto , o bloco volta a subir por uma segunda rampa de altura até uma plataforma horizontal. Esta plataforma possui atrito e o bloco desliza até parar no ponto . O coeficiente de atrito cinético na plataforma vale .

Use para a aceleração da gravidade. As variáveis dadas do problema são (, , , , e )

a) Determine a compressão da mola em termos das variáveis dadas do problema.

b) Determine a velocidade do bloco no ponto em termos das variáveis do problema.

c) Determine a distância percorrida na plataforma em termos das variáveis dadas.

d) Calcule a menor altura de modo que acima dela o bloco volta a tocar na mola.