P3 de Física 1 - FIS1033 da PUCRIO - 2018.1

Dois cilindros de raios diferentes são unidos conforme a figura, sendo o raio do cilindro menor e do cilindro maior . Fios ideais, que não escorregam, são enrolados em cada um dos cilindros e na outra extremidade de cada um dos fio é pendurada uma massa . Este sistema é colocado para girar ao redor de um eixo de rotação horizontal, sem atrito. O momento de inércia deste sistema torno do eixo vale . O sistema inicialmente se encontra em repouso. Após deixarmos os pesos cair, determine a aceleração angular deste sistema utilizando as leis de Newton em termos de , a aceleração da gravidade, e de . NÃO substitua por valores numéricos.

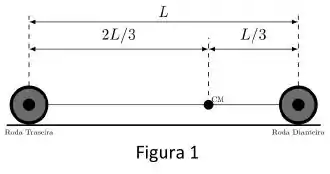
Considere o modelo simplificado de um carro descrito pela figura 1, que possui apenas duas rodas: uma traseira e uma dianteira. A distância entre as duas rodas é dada por . O centro de massa do carro se encontra no ponto de distância de distância da roda traseira. .

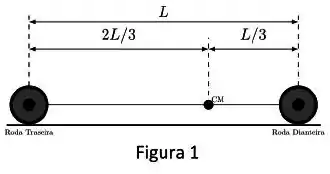
a) Sabendo que o carro completo tem massa de , calcule o valor das forças normais: da roda dianteira e na roda traseira , na situação de equilíbrio estático e repouso.

Dados:

Um disco (1), de massa , raio e momento de inércia ao redor de seu centro de massa , desliza em um plano horizontal, sem atrito, com velocidade e velocidade angular (veja a figura), onde o eixo se situa para fora da folha. Em , o disco 1 colide com um disco 2 idêntico a ele, de modo que os dois saem grudados em suas extremidades.

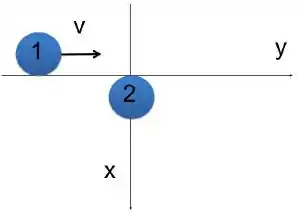
a) Dentre as grandezas seguintes: energia cinética, momento linear e momento angular, diga quais se conservam, e quais não se conservam. Justifique.

b) Calcule a velocidade do centro de massa do sistema formado pelos dois discos antes e depois da colisão.

c) Descreva o movimento do sistema formado pelos dois discos grudados após a colisão, e calcule a velocidade angular final dos discos após a colisão.

Considere o modelo simplificado de um carro descrito pela figura 1, que possui apenas duas rodas: uma traseira e uma dianteira. A distância entre as duas rodas é dada por . O centro de massa do carro se encontra no ponto de distância de distância da roda traseira. .

De agora em diante considere que ambas as rodas possuem raio , massa e momento de inércia ao redor do centro de massa . No item (b) existe atrito entre as rodas e o chão, e elas rolam sem deslizar.

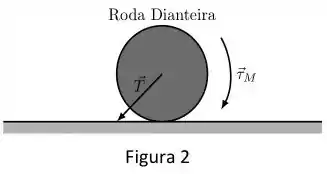
b) A figura 2 descreve uma versão simplificada da roda dianteira em movimento. O motor realiza sobre ela um torque (para dentro da folha). A força (SI) é a força que o veículo faz sobre a roda, que é aplicada diretamente no centro de massa da roda. Calcule a aceleração angular da roda. Cuidado ao escolher a direção da força de atrito.

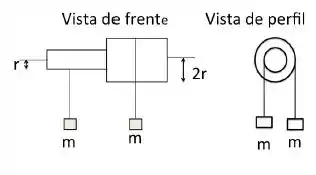
O sistema da figura ao lado é constituído por uma barra homogênea de comprimento , e massa , e um anel de raio e massa . Este anel está fixo em uma das extremidades da barra e a outra extremidade pode girar em torno de um eixo de rotação horizontal. Inicialmente o sistema se encontra em repouso, com a barra e o anel em um plano horizontal. O objeto então é liberado e pode girar livremente, sem atrito, em torno do eixo (a figura mostra o objeto na parte mais baixa de sua trajetória)

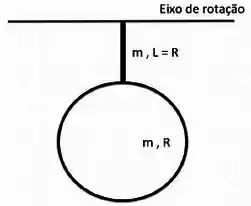
a) Calcule o momento de inércia do objeto em relação ao eixo descrito (dados: momento de inércia da barra em torno de seu centro de massa , momento de inércia do anel com eixo de rotação ao redor de um diâmetro ).

b) Calcule a velocidade angular do objeto ao passar na parte mais baixa da trajetória (Lembre-se, quando a barra se encontra na horizontal o objeto esta em repouso).