Parte III:
Uma força atua sobre o bloco conforme a figura ao lado, produzindo o movimento dos blocos , e juntos sobre uma superfície áspera com coeficiente de atrito cinético . As massas desses blocos são respectivamente, e .
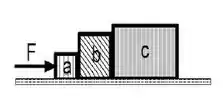
(e) Determine a força que o bloco faz sobre o .
1-( )
2-( )
3-( )
4-( )
5-( )
Passo 1
Temos uma força no bloco . O bloco vai empurrar o bloco , que por sua vez, vai empurrar o bloco . Ou seja, vai existir uma força normal de contato entre cada dois blocos.
Além disso, a superfície é áspera. Logo, vai existir uma força de atrito em cada bloco com o chão, e seu coeficiente de atrito cinético é .
Os três blocos vão andar juntos. Então vamos descobrir a aceleração desse movimento, considerando esse sistema como apenas um grande blocão com massa .
Nesse caso, a força normal com o chão se cancela com a força peso, então :
A soma das massas é igual a :
Passo 2
Agora que achamos a aceleração , que vai ser também a aceleração de cada bloco, talvez você pense em aplicar a segunda lei de Newton no bloco , e com isso encontrar a força que o bloco aplica em . Porém, dá uma olhada no somatório de forças no bloco :
Temos uma força normal desconhecida de cada lado, então vamos ter que pegar um dos blocos ou para fazer o somatório de forças.
Vamos escolher o bloco , já que ele tem menos forças sendo aplicadas sobre ele.
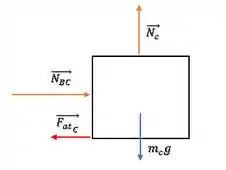
Como a força normal com o chão se anula com a força peso :
Encontramos a força normal que faz em . Mas os dois blocos não se empurram com a mesma força (ação e reação)?
Sim! Então, a força que faz em vai ser igual em módulo com .
Vamos calcular o valor com números, agora:
Para finalizar, não podemos esquecer a direção da nossa força. Se é a força com que empurra , ela aponta para a esquerda. Logo, o vetor vai ser na componente negativa:
Resposta
1-( )
2-( )
3-(V)
4-( )
5-( )