Parte II:
Uma partícula P se move com velocidade escalar constante sobre uma circunferência de raio (figura abaixo) e completa uma volta a cada . A partícula passa pelo ponto no instante . Nesse mesmo instante um atleta A passa pelo mesmo ponto com velocidade constante, correndo ao longo do eixo . O ponto designa a origem de um referencial () em repouso em relação ao solo. Expresse os resultados em função dos vetores unitários.
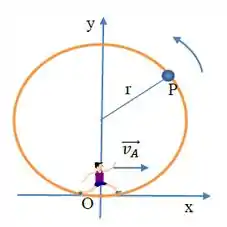
(a ) Encontre a posição da partícula em relação a , nos instantes e .
(b ) Obtenha o deslocamento da partícula entre 𝑒 .
(c ) Calcule a velocidade da partícula no instante .
(d ) Determine a velocidade da partícula em relação ao atleta no instante . Admita que o atleta A possui a mesma velocidade da partícula P na origem do referencial .
Passo 1
Temos a partícula P realizando uma trajetória circular e com velocidade escalar constante, logo, estamos tratando de um movimento circular uniforme (MUC). Além disso, ela completa cada volta em , então seu período é de .
Vamos resolver cada item, então. Chega mais!
Passo 2
(a ) Encontre a posição da partícula em relação a , nos instantes e .
Primeiro, vamos pensar no período da partícula. Se ela completa uma volta a cada , em ela vai ter completado um quarto de volta e em , metade de uma volta.
Então a nossa partícula vai estar nas seguintes posições:
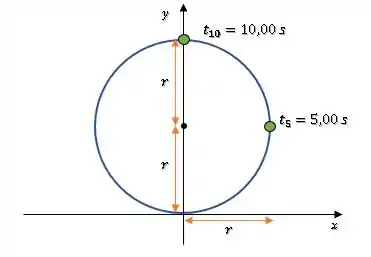
Se o raio () mede , então podemos escrever a posição de cada partícula com suas coordenadas em e :
Ou então:
Onde, esses seriam os vetores posição e :
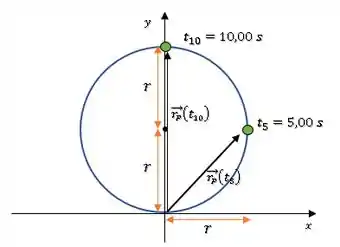
Passo 3
(b ) Obtenha o deslocamento da partícula entre 𝑒 .
O deslocamento será o vetor :
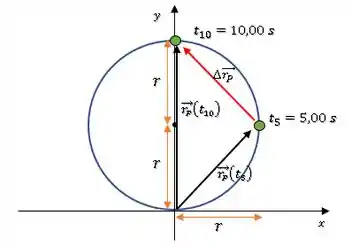
Para obtermos o delocamento, precisamos apenas subtrair o vetor da posição final menos o da posição inicial:
Passo 4
(c ) Calcule a velocidade da partícula no instante .
A velocidade da partícula ao longo do trajeto é sempre tangencial ao círculo. Em , a partícula está em um quarto de volta da circunferência, então, sua velocidade estará assim:
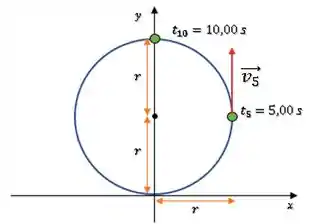
Logo, a velocidade em está na vertical e aponta para cima (componente ).
Para calcular o módulo da velocidade, podemos usar a fórmula de velocidade média, já que a partícula anda sempre com a mesma velocidade:
Em um período de , a partícula percorre o comprimento da circunferência (:
Assim, temos que:
Passo 5
(d ) Determine a velocidade da partícula em relação ao atleta no instante . Admita que o atleta A possui a mesma velocidade da partícula P na origem do referencial .
Qual a ideia aqui?
O atleta se movimenta em relação à origem, certo? Certo!
Mas se considerarmos o referencial no atleta, temos que a origem se movimenta em relação ao atleta, certo? Certo!
O mesmo acontece entre a partícula e a origem. Mas precisamos achar a velocidade da partícula em relação ao atleta. Então, é como se a gente deixasse o atleta fixo, pegasse a sua velocidade na direção contrária e somasse com a velocidade da partícula. Desse forma eles terão a mesma velocidade de afastamento/aproximação entre eles.
Logo, a velocidade de P com relação a A (), no instante , vai ser a velocidade de P com relação à origem () menos a velocidade de A com relação a origem():
Sabemos que o módulo da velocidade do atleta () é igual ao da partícula, porém ele se mantém sempre na direção do eixo , logo:
Agora, podemos substituir e , no instante :
Resposta
(a)
(b)
(c)
(d)