P2 de Física 1 - FIS1033 da PUCRIO - 2009.2

Um pêndulo balístico é um dispositivo utilizado para medir a velocidade de um projétil quando ele deixa o cano de uma arma. Esta velocidade é chamada de velocidade de saída do projétil. Um projétil de massa é disparado horizontalmente contra um bloco de madeira de massa que forma o peso de um pêndulo. O projétil penetra no bloco e o observador mede então a altura máxima atingida pelo conjunto formado pelo bloco e pelo projétil. Responda:

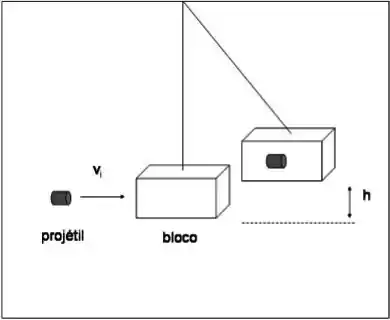
a) alguma grandeza é conservada nesta colisão? Por que?

b) qual é a velocidade do sistema projétil + bloco imediatamente após a colisão sabendo que o sistema atinge a altura máxima de ?

c) qual é a velocidade inicial do projétil?

Vamos supor que duas partículas e colidem bidimensionalmente. Seja a partícula de massa e a partícula de massa . As posições das partículas num certo instante antes da colisão são dadas por e . O tempo de duração da colisão é de .

a) Calcule o vetor de posição do centro de massa no instante .

b) Suponha agora que as velocidades no início da colisão são: e , e que no fim da colisão a componente da velocidade de é igual a e a componente da velocidade de é . Escreva os vetores velocidade de ambas as partículas no fim da colisão.

c) Suponha agora que as velocidades no início da colisão são: e , e que a colisão é completamente inelástica. Calcule o vetor força média que atua na partícula durante a colisão ().

Dois blocos e com massas de e estão ligados através de uma corda e de uma polia sem atrito de massas desprezíveis. Veja o desenho ao lado. A distância entre os pontos e indicados na figura é de . Existe atrito entre o bloco e o plano inclinado e o coeficiente de atrito cinético é igual a . Os blocos são soltos a partir do repouso.

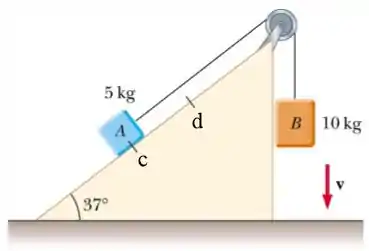
a) Calcule o trabalho realizado pela força da gravidade nos blocos e quando o bloco percorre a distância entre os pontos e .

b) Calcule a variação das energias cinética e potencial do sistema quando o bloco percorre a distância entre os pontos e .

c) Suponha agora que a partir de uma outra condição inicial o bloco chegue ao ponto com uma velocidade de e que neste instante o bloco tenha sua energia mecânica totalmente dissipada na colisão com o solo. Calcule a distância percorrida até que o bloco pare.

d) Finalmente suponha que no trecho entre os pontos e o atrito variasse linearmente com a distância percorrida, de tal forma que em a força de atrito fosse nula e em a força de atrito fosse igual a . Calcule o trabalho realizado pelo atrito sobre o corpo nestas condições.