Dois blocos e com massas de e estão ligados através de uma corda e de uma polia sem atrito de massas desprezíveis. Veja o desenho ao lado. A distância entre os pontos e indicados na figura é de . Existe atrito entre o bloco e o plano inclinado e o coeficiente de atrito cinético é igual a . Os blocos são soltos a partir do repouso.

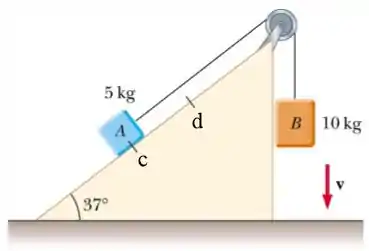
a) Calcule o trabalho realizado pela força da gravidade nos blocos e quando o bloco percorre a distância entre os pontos e .

b) Calcule a variação das energias cinética e potencial do sistema quando o bloco percorre a distância entre os pontos e .

c) Suponha agora que a partir de uma outra condição inicial o bloco chegue ao ponto com uma velocidade de e que neste instante o bloco tenha sua energia mecânica totalmente dissipada na colisão com o solo. Calcule a distância percorrida até que o bloco pare.

d) Finalmente suponha que no trecho entre os pontos e o atrito variasse linearmente com a distância percorrida, de tal forma que em a força de atrito fosse nula e em a força de atrito fosse igual a . Calcule o trabalho realizado pelo atrito sobre o corpo nestas condições.

b)

Aplicando o teorema trabalho-energia:

Substituindo:

Podemos encontrar a força normal em fazendo o equilíbrio com a componente do peso, . Então:

Para a variação da energia potencial, temos que o bloco ganhou de energia potencial já que ele ganhou altura e o bloco perdeu de energia potencial já que ele perdeu altura. Então a variação da energia potencial do sistema foi:

c)

Basta aplicar o teorema trabalho-energia novamente

d)

O módulo do trabalho do atrito é a área sob o gráfico, força x deslocamento.

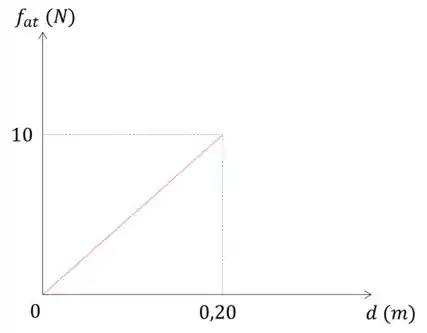
Como o deslocamento tem sentido oposto ao da força do atrito