P3 de Física 1 - FIS1033 da PUCRIO - 2017.1

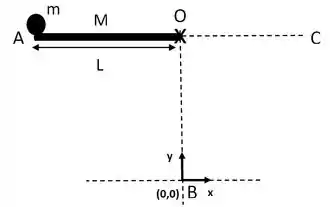
A figura mostra um sistema mecânico simples. Uma haste delgada de massa e comprimento está presa em uma extremidade por um pino e livre para girar sem atrito. Na outra extremidade se encontra presa uma esfera de massa e raio desprezível. Considere e a distância vertical

Dados:

-

-

-

-

Determine

1. Uma expressão literal para o momento de inércia do sistema em relação ao ponto fixo , contendo somente as variáveis indicadas no enunciado.
2. Um valor numérico para este momento de inércia.
3. O momento angular total do sistema ao passar pelo ponto B.

Um bloco de massa encontra-se suspenso por uma corda ideal que passa por uma roldana de raio , com momento de inércia . A corda encontra-se enrolada ao cilindro central de um carretel na outra extremidade. O bloco é liberado a partir do repouso. A roldana e o carretel podem girar livremente (sem atrito) em torno de seus eixos fixos. Os centros de massa dos carretéis estão em repouso, não transladam.

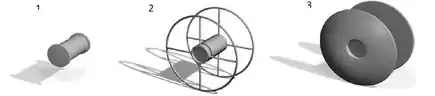
1. Considere os três carretéis abaixo feitos de materiais diferentes, com formas diferentes, de modo a terem a mesma massa. As distribuições de massa são homogêneas nas partes sólidas. Os três carretéis possuem o mesmo cilindro central. Com qual dos carretéis o bloco teria o menor valor da aceleração? Justifique sua resposta.



2. Calcule o momento de inércia do carretel , considerando que cada uma das hastes é delgada, tem massa 𝑀 e comprimento . Os anéis são finos com massa 𝑀 e raio 𝑅. O cilindro central possui massa e raio .
3. Sabendo-se que o carretel utilizado foi o . Qual a aceleração adquirida pelo bloco durante sua queda? Admita , , , , e .

Uma roda homogênea é constituída por um disco maciço, uniforme, de massa , com um orifício de raio externo e raio interno . Há um eixo encaixado nele rigidamente (veja a figura).

O eixo que passa pelo orifício é cilíndrico, maciço, homogêneo, tem raio e a mesma massa . O momento de inércia do conjunto roda-eixo em relação ao centro de massa do eixo é . A roda está inicialmente em repouso no alto de uma rampa que faz um ângulo , pequeno, com a horizontal. Essa rampa possui um sulco aberto e largo no qual a roda se encaixa, sem tocá-la. O eixo está apoiado na rampa.

Após ser liberada, a roda rola suavemente, sem deslizamento, para baixo com seu centro de massa descendo uma distância .

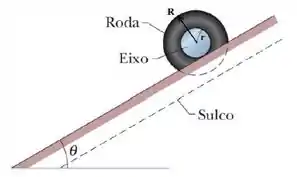
1. Determine uma expressão literal para o valor da velocidade angular da roda no final da distância , em função dos dados citados. Sugestão: faça por energia.
2. Determine uma expressão literal para o valor da força de atrito estático sobre da roda durante a descida em função dos dados citados.

Considere uma roda de massa , raio e momento de inércia girando com velocidade angular inicial , sentido horário, baixada sobre uma superfície plana horizontal rugosa com seu centro de massa em repouso inicialmente. O coeficiente de atrito cinético entre a roda e o plano é . A seguir a roda se move no sentido positivo do eixo , deslizando e girando durante um intervalo de tempo . Após o instante de tempo , segue rolando sem deslizar.

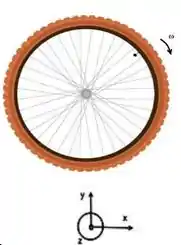
Indique no desenho, as forças que agem sobre a roda durante . Determine na forma literal uma expressão para o coeficiente de atrito cinético em função dos dados citados.

A figura mostra um sistema mecânico simples. Uma haste delgada de massa e comprimento está presa em uma extremidade por um pino e livre para girar sem atrito. Na outra extremidade se encontra presa uma esfera de massa e raio desprezível. Considere e a distância vertical

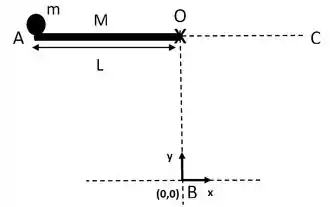
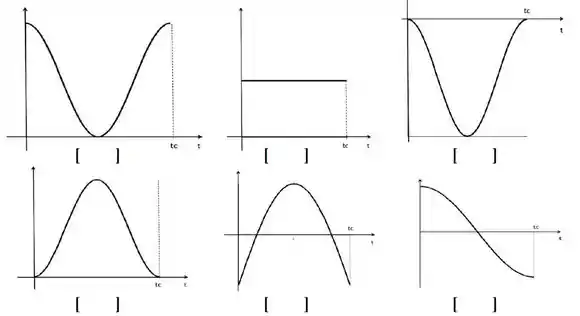
Considere agora o movimento do sistema abandonado do repouso no ponto A. Indique com o número apropriado o gráfico que representa cada uma das grandezas físicas do movimento em função do tempo até que o sistema finalmente alcance novamente o repouso no ponto C.

[1] O Momento Angular Total do Sistema.

[2] O Torque que Atua no Sistema

[3] A Energia Potencial Gravitacional.

[4] A Energia Mecânica Total

[5] A variação da Energia Potencial Gravitacional.