UFPE- Física geral 1 – P2 2019.2
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.
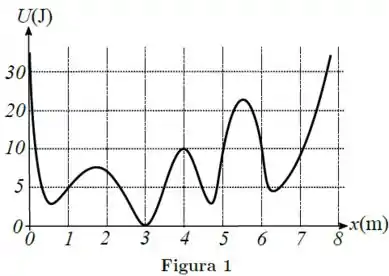
Ao passar pela posição , a velocidade da partícula é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Como não há forças dissipativas, temos que a energia mecânica do sistema se conserva, desse modo, vamos analisar a conservação da energia mecânica entre os pontos 1 e 3:
Pelo gráfico, temos:
O enunciado nos diz que a velocidade da partícula em é . Então, a energia cinética em 1 é:
Então:
Que é a letra e).
Resposta
Letra e).
Exercícios de Livros Relacionados
Uma única força conservativa F ( x ) age sobre uma partícula de 1,0k g que se move ao longo de um eixo x . A energia potencial U ( x ) associada a F ( x ) é dada por U x = - 4 x e - x 4J onde x está e
A energia potencial entre dois átomos de hidrogênio separados por uma distância x muito grande é dada por U x = - C 6 / x 6 , onde C 6 é uma constante positiva. Qual é a força que um átomo exerce sobr
Duas massas, m 1 e m 2 , estão sobre o eixo x, sendo m1 mantido no lugar de origem e m 2 naposição x, livre para se mover. A energia potencial gravitacional dessas massas é dada por U x = - G m 1 m 2
A massa do Ônibus Espacial orbital é cerca de 8 × 10 4k g e o período de sua órbita é 90 min. Estime a energia cinética da nave e o trabalho realizado pela gravidade sobre ela entre o lançamento e a e
A força atrativa entre dois núcleons (prótons ou nêutrons) é descrita com boa aproximação pelo potencial de Yukawa V r = - V o r o r e - r r o Onde V o = 8,0x10 - 12 J ,r o = 1,5x10 - 15m e r é a dist