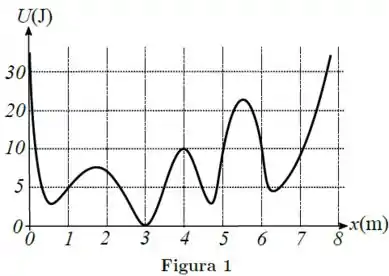
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.
Considere as afirmativas abaixo:
(I) A força em é positiva (isto é, no sentido positivo do eixo ).
(II) O trabalho realizado pela força entre e é positivo.
(III) A variação da energia mecânica entre e é negativa.
Marque a alternativa que contém apenas afirrmativa(s) verdadeira(s).
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Passo 1
Vamos analisar cada uma das afirmativas!
(I) A força em é positiva (isto é, no sentido positivo do eixo ).
Quando temos essas questões de gráfico de , uma relação muito importante é:
Ou seja, a força é menos a inclinação do gráfico.
Vamos ver, por exemplo, em , temos que a curva tá “subindo”, então . Pois a derivada é a inclinação da reta tangente naquele ponto.
Mas como
Temos que nesse ponto
Portanto essa tá errada!
Passo 2
(II) O trabalho realizado pela força entre e é positivo.
O trabalho de uma força conservativa é dado por
Olhando no gráfico temos que e , então
Então o trabalho:
Opa! O trabalho deu negativo, então essa também está errada!
Passo 3
(III) A variação da energia mecânica entre e é negativa.
Falsa!! A energia mecânica se conserva, pois o enunciado diz que não há forças dissipativas para roubar energia do sistema. Portanto, a variação da energia mecânica é nula!
Portanto, nenhuma afirmativa é verdadeira.
Resposta
Letra h)