Um bloco de massa encontra-se inicialmente mantido em repouso, comprimindo de uma mola de constante elástica (ver Figura 3). Quando o bloco liberado, ele perde contato com a mola antes do ponto . Não existe atrito antes do ponto .

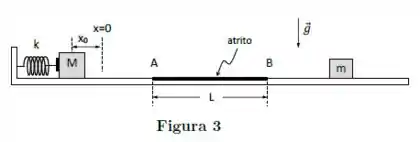
(a) Calcule a velocidade do bloco no ponto .

(b) Entre os pontos e o bloco atravessa uma região de comprimento com Coeficiente de atrito cinético . Calcule o trabalho realizado pela força de atrito nessa região. Considere .

(c) Calcule a velocidade do bloco no ponto

(d) Após o ponto , o atrito deixa de existir e o bloco realiza uma colisão perfeitamente inelástica com um outro bloco de massa que se encontrava inicialmente parado. Calcule a velocidade dos blocos após a colisão.

(b) Entre os pontos e o bloco atravessa uma região de comprimento com coeficiente de atrito cinético . Calcule o trabalho realizado pela força de atrito nessa região.

O trabalho de uma força é dado pelo produto escalar entre a força e o deslocamento:

Então

E como a força de atrito é oposta ao deslocamento, temos que oproduto interno entre esses vetores dará:

Mas, .

Então

Assim,

O deslocamento vale , que é o pedaço que o bloco anda com o atrito atuando.

Substituindo os valores:

c) Calcule a velocidade do bloco no ponto

Bom, a força de atrito retira energia do sistema, então não podemos fazer por conservação de energia.

Mas a quantidade de energia que a força de atrito rouba do sistema é exatamente igual ao trabalho dela. Ou seja,

Esse é o teorema trabalho-energia cinética.

Já vimos que

Substituindo:

Então, resolvendo:

(d) Após o ponto , o atrito deixa de existir e o bloco realiza uma colisão perfeitamente inelástica com um outro bloco de massa que se encontrava inicialmente parado. Calcule a velocidade dos blocos após a colisão.

Em uma colisão perfeitamente inelástica os corpos saem colados no final, isso quer dizer que eles possuem a mesma velocidade final.

O momento linear se conserva, pois não temos forças externas atuando , então

Então