Um projétil de massa incide com velocidade inicial sobre um alvo de massa , inicialmente parado sobre uma superfície horizontal sem atrito. O alvo tem forma curva na área atingida pelo projétil, conforme mostra a Figura 2. Ao perder o contato com o alvo, o projétil possui velocidade . Devido ao contato com o projétil, o alvo passa a se mover horizontalmente para a direita. Despreze os efeitos da gravidade sobre o movimento do projétil.
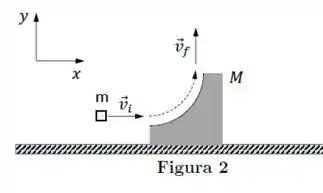
Seja a velocidadedo alvo no instante final em que ele perde contato com o projétil. A variação do momento linear do alvo entre os instantes inicial e final é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
A variação de qualquer grandeza é a subtração da quantidade final pela quantidade inicial, ou seja, no nosso caso:
Mas, no inicio, o alvo estava parado, então
Assim:
Substituindo
Que é a letra e!
Resposta
Letra e).