Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.

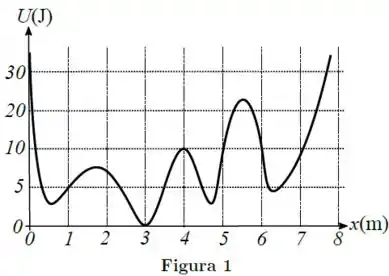
Além de um ponto de retorno no intervalo, em que a energia cinética da partícula é nula, há também um outro ponto de retorno no intervalo (em metros):

(a)

(b)

(c)

(d)

(e)

(f)

(g)

O enunciado nos diz que entre temos um ponto de retorno. Mas o que isso quer dizer?

Quer dizer que a energia mecânica é puramente a energia potencial.

No ponto 1, que é onde o movimento se origina, temos

Pelo gráfico, vemos que: .

E além disso, podemos calcular a energia cinética em 1, pelos dados do enunciado:

Com isso, a energia mecânica em 1 é:

Beleza!

Então essa é a nossa energia mecânica, que significa um limite, ou seja, não podemos ter uma energia potencial, ou cinética maior que , pois .

Mas notem que entre a região o gráfico da energia potencial passa de . Então é nessa região que temos um ponto de retorno, ok?