3º EE de Física 1 da UFPE - 2018.2

Três partículas de massa estão presas a hastes de tamanho e massas desprezíveis, como uma hélice. O sistema pode girar em torno de um eixo fixo que passa pelo seu centro, , e inicialmente possui velocidade angular . Um chiclete de massa incide com velocidade conforme a figura, e realiza uma colisão perfeitamente inelástica com uma das massas .

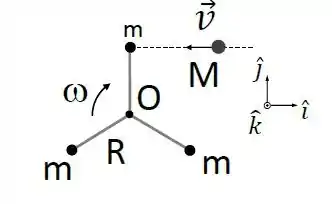
Julgue as seguintes assertivas

I. O momento de inércia do sistema composto pelas 3 massas é em relação ao eixo de rotação.

II. O momento angular inicial do sistema composto pelas 3 massas m aponta na direçãoem relação ao eixo de rotação.

III. O momento angular da massa antes da colisão tem módulo em relação ao eixo de rotação.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

(A) I

(B) II

(C) III

(D) I e II

(E) I e III

(F) II e III

(G) Todas

(H) Nenhuma

Três partículas de massa estão presas a hastes de tamanho e massas desprezíveis, como uma hélice. O sistema pode girar em torno de um eixo fixo que passa pelo seu centro, , e inicialmente possui velocidade angular . Um chiclete de massa incide com velocidade conforme a figura, e realiza uma colisão perfeitamente inelástica com uma das massas .

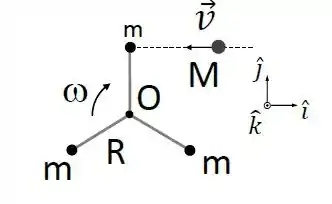
Considere que . Para que o sistema pare completamente após a colisão é necessário que tenha módulo

(A)

(B)

(C)

(D)

(E)

(F)

(G)

(H)

Uma roda de massa e raio rola sem deslizar sobre uma superfície horizontal com

atrito ao ser puxada por uma força, aplicada sobreo seu eixo. O coeficiente de atrito entre a roda e a superfície é , e a velocidade do centro de massa é. O momento de inércia total da roda éem torno do eixo que passa pelo seu centro de massa.

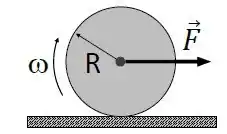
Julgue as seguintes assertivas

I. Na ausência de deslizamento, .

II. A energia cinética total da roda é.

III. Quando a força , é constante e a força de atrito é nula.

É correto apenas o que se afirma em

(A) I

(B) II

(C) III

(D) I e II

(E) I e III

(F) II e III

(G) Todas

(H) Nenhuma

Uma roda de massa e raio rola sem deslizar sobre uma superfície horizontal com

atrito ao ser puxada por uma força , aplicada sobreo seu eixo. O coeficiente de atrito entre a roda e a superfície é , e a velocidade do centro de massa é . O momento de inércia total da roda éem torno do eixo que passa pelo seu centro de massa.

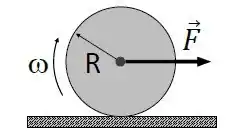
Considere que e . O maior valor do módulo da aceleração angular para o qual a roda não desliza é:

(A)

(B)

(C)

(D)

(E)

(F)

(G)

(H)

Uma partícula de massa amarrada a um barbante de massa desprezível gira sobre uma mesa sem atrito, percorrendo uma circunferência de raio em torno do ponto . A pessoa que segura o barbante diminui lentamente o raio da circunferência até que .

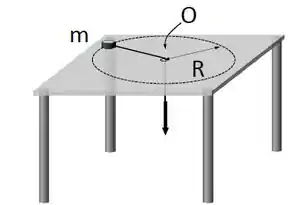
Se a velocidade angular inicial da partícula, sua velocidade angular final é:

(A)

(B)

(C)

(D)

(E)

(F)

(G)

(H)

Uma partícula de massa amarrada a um barbante de massa desprezível gira sobre uma mesa sem atrito, percorrendo uma circunferência de raio em torno do ponto . A pessoa que segura o barbante diminui lentamente o raio da circunferência até que .

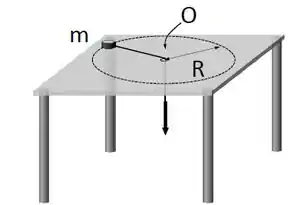
Considere as seguintes afirmativas relativas ao movimento da partícula:

I. O momento angular da partícula em relação a se conserva.

II. A velocidade angular da partícula em torno de aumenta.

III. O momento de inércia da partícula em relação a diminui.

É correto apenas o que se afirma em:

(A) I

(B) II

(C) III

(D) I e II

(E) I e III

(F) II e III

(G) Todas

(H) Nenhuma

Um pequeno bloco de massa parte do repouso e desliza para baixo numa superfície curva sem atrito a partir de uma altura e depois adere a uma barra homogênea de massa e comprimento . A barra, inicialmente em repouso na vertical, então gira sem atrito em torno do eixo fixo de um ângulo antes de parar momentaneamente.

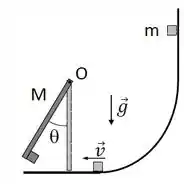
(A) Determine a velocidade do bloco após descer a superfície curva.

(B) Calcule o módulo do momento angular da massa em relação ao ponto , imediatamente antes do choque com a barra.

(C) Calcule o momento de inércia do conjunto barra + bloco em relação ao ponto .

(D) Calcule a velocidade angular do conjunto barra + bloco imediatamente depois do choque.

Dado: o momento de inércia de uma barra delgada de comprimento e massa girando sobre um eixo perpendicular à barra, passando por seu centro de massa é.